What Is 3/24 As A Percent
listenit
May 12, 2025 · 4 min read
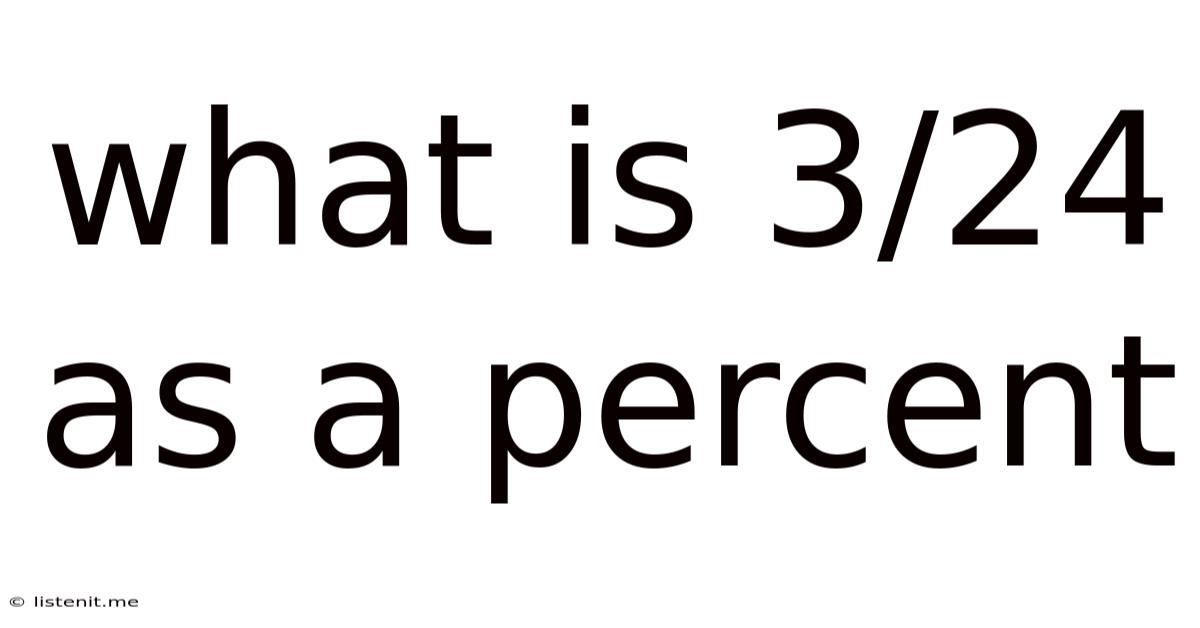
Table of Contents
What is 3/24 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with applications across various fields, from finance and statistics to everyday life. This comprehensive guide will delve into the process of converting the fraction 3/24 into a percentage, explaining the steps involved and providing additional examples to solidify your understanding. We'll also explore the broader context of fraction-to-percentage conversion and its practical relevance.
Understanding Fractions and Percentages
Before diving into the conversion, let's refresh our understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts the whole is divided into. In our case, 3/24 means we have 3 parts out of a total of 24 parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2.
Converting 3/24 to a Percentage: Step-by-Step
The conversion process involves two primary steps: simplifying the fraction and then converting the simplified fraction to a percentage.
Step 1: Simplifying the Fraction
The fraction 3/24 can be simplified by finding the greatest common divisor (GCD) of the numerator (3) and the denominator (24). The GCD of 3 and 24 is 3. Dividing both the numerator and the denominator by the GCD, we get:
3 ÷ 3 = 1 24 ÷ 3 = 8
Therefore, the simplified fraction is 1/8.
Step 2: Converting the Simplified Fraction to a Percentage
To convert a fraction to a percentage, we multiply the fraction by 100%. In this case:
(1/8) * 100% = 100/8 %
Now, we perform the division:
100 ÷ 8 = 12.5
Therefore, 3/24 is equal to 12.5%.
Alternative Method: Direct Conversion
While simplifying the fraction first is generally recommended for easier calculations, you can also directly convert the original fraction to a percentage:
(3/24) * 100% = 300/24 %
Then, simplify the resulting fraction:
300 ÷ 24 = 12.5
This confirms that 3/24 is indeed equal to 12.5%.
Practical Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages is vital in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, and profit margins often involves converting fractions to percentages. For example, if a bank offers a loan with an interest rate of 1/20, converting this fraction to a percentage (5%) helps in understanding the cost of borrowing.
-
Statistics: Expressing data as percentages helps in visualizing and interpreting results. For example, if a survey shows that 3 out of 24 respondents prefer a particular product, converting this to a percentage (12.5%) provides a clearer understanding of the product's popularity.
-
Everyday Life: Numerous everyday situations require fraction-to-percentage conversion. Calculating tips in restaurants, determining sale discounts, or understanding the completion percentage of a task all benefit from this skill.
Further Examples of Fraction-to-Percentage Conversions
Let's explore a few more examples to reinforce the concept:
Example 1: Converting 5/20 to a percentage
- Simplify the fraction: 5/20 simplifies to 1/4.
- Convert to percentage: (1/4) * 100% = 25%
Therefore, 5/20 is equal to 25%.
Example 2: Converting 7/14 to a percentage
- Simplify the fraction: 7/14 simplifies to 1/2.
- Convert to percentage: (1/2) * 100% = 50%
Therefore, 7/14 is equal to 50%.
Example 3: Converting 15/60 to a percentage
- Simplify the fraction: 15/60 simplifies to 1/4.
- Convert to percentage: (1/4) * 100% = 25%
Therefore, 15/60 is equal to 25%.
Example 4: Converting 1/3 to a percentage
- This fraction doesn't simplify further.
- Convert to percentage: (1/3) * 100% ≈ 33.33% (repeating decimal)
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a crucial mathematical skill with wide-ranging applications. By understanding the steps involved, practicing with various examples, and recognizing the practical relevance of this conversion, you can confidently handle percentage-related calculations in various aspects of your life. Remember, the key lies in simplifying the fraction whenever possible to make the calculation smoother and less prone to errors. Mastering this skill empowers you to analyze data more effectively, make informed decisions, and confidently navigate numerical challenges in your academic pursuits and professional life. Regular practice will solidify your understanding and improve your speed and accuracy in tackling these conversions.
Latest Posts
Latest Posts
-
Find Height Of An Isosceles Triangle
May 12, 2025
-
What Element Has 16 Protons And 18 Electrons
May 12, 2025
-
Difference Between Percent Abundance And Relative Abundance
May 12, 2025
-
Give The Hybridization For The Br In Brcl3
May 12, 2025
-
What Is The Binomial Expansion Of 2x 3 5
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/24 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.