What Is 20 Off Of 300
listenit
May 21, 2025 · 5 min read
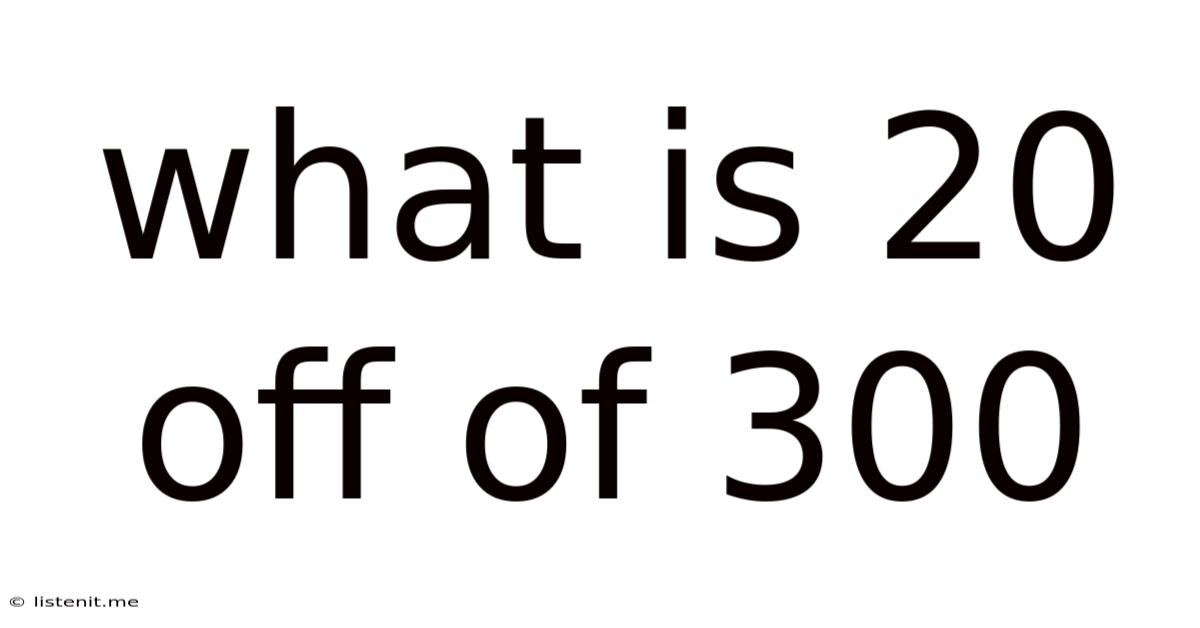
Table of Contents
What is 20% Off of 300? A Comprehensive Guide to Percentage Calculations
Calculating discounts is a common task in everyday life, whether you're shopping for groceries, planning a vacation, or simply trying to understand a sale. Understanding how percentages work is crucial for making informed financial decisions. This article delves into the calculation of "20% off of 300," providing not only the answer but also a thorough explanation of the underlying principles and various methods to solve similar problems. We’ll explore different approaches, making this concept accessible to everyone, regardless of their mathematical background.
Understanding Percentages: The Basics
Before we tackle the specific problem, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 20% means 20 out of 100, which can also be written as the fraction 20/100 or the decimal 0.20.
This understanding is fundamental to solving percentage-based problems like calculating discounts. The core concept is to translate the percentage into a usable form, usually a decimal or fraction, to perform the necessary arithmetic.
Method 1: Converting Percentage to Decimal
This is arguably the most straightforward method for calculating discounts. We convert the percentage (20%) into its decimal equivalent (0.20) and then multiply it by the original price (300).
Steps:
- Convert the percentage to a decimal: Divide the percentage by 100. 20% / 100 = 0.20
- Multiply the decimal by the original price: 0.20 * 300 = 60
Therefore, a 20% discount on 300 is $60.
Finding the final price: To find the final price after the discount, subtract the discount amount from the original price: 300 - 60 = 240.
So, 20% off of 300 is $240.
Advantages of this method:
- Simplicity: This method is easy to understand and implement, even for those with limited mathematical skills.
- Direct Calculation: It provides a direct calculation of the discount amount, making it easy to understand the savings.
- Wide Applicability: This approach is universally applicable to all percentage discount calculations.
Disadvantages of this method:
- Multiple Steps: It involves a two-step process (conversion and multiplication). While simple, it requires two distinct calculations.
Method 2: Converting Percentage to Fraction
This method uses the fraction equivalent of the percentage. 20% can be expressed as 20/100, which simplifies to 1/5.
Steps:
- Convert the percentage to a fraction: 20% = 20/100 = 1/5
- Multiply the fraction by the original price: (1/5) * 300 = 60
This gives us the same discount amount of $60.
To find the final price: 300 - 60 = 240
So, 20% off of 300 is $240.
Advantages of this method:
- Conceptual Understanding: This approach reinforces the understanding of percentages as fractions, which can be helpful in grasping the underlying mathematical concept.
- Mental Calculation (for simpler percentages): For simpler percentages like 20%, 50%, or 25%, this method can facilitate quicker mental calculations.
Disadvantages of this method:
- Fraction Simplification: Requires the ability to simplify fractions, which might be challenging for some individuals.
- Less Efficient for Complex Percentages: This method becomes less efficient when dealing with more complex percentages that don't simplify to easy fractions.
Method 3: Using the Complement
This method focuses on finding the remaining percentage after the discount. If there's a 20% discount, then 80% (100% - 20%) of the original price remains.
Steps:
- Calculate the remaining percentage: 100% - 20% = 80%
- Convert the remaining percentage to a decimal: 80% / 100 = 0.80
- Multiply the decimal by the original price: 0.80 * 300 = 240
This directly gives us the final price after the discount.
So, 20% off of 300 is $240.
Advantages of this method:
- Direct Final Price Calculation: This method provides the final price in a single step, avoiding the need for a separate subtraction step.
- Efficiency: This is often the most efficient method, especially when calculating multiple discounts or taxes.
Disadvantages of this method:
- Slightly Less Intuitive: It might be slightly less intuitive for beginners as it involves understanding the concept of the complement (remaining percentage).
Solving Similar Problems: A Practical Approach
Now that we understand the different methods, let's apply this knowledge to solve similar problems. Let's say you want to calculate 15% off of $450. Using the decimal method:
- Convert the percentage to a decimal: 15% / 100 = 0.15
- Multiply by the original price: 0.15 * 450 = 67.50
- Subtract the discount from the original price: 450 - 67.50 = 382.50
Therefore, 15% off of $450 is $382.50.
You can use any of the methods discussed above to tackle different percentage discount scenarios. The choice of method ultimately depends on personal preference and the specific context of the problem. However, for efficiency and simplicity, the decimal method often proves to be the most reliable and straightforward.
Beyond Discounts: Applying Percentage Calculations in Real-Life Scenarios
Understanding percentage calculations extends far beyond simple discounts. Here are some real-life applications:
- Sales Tax: Calculating sales tax on purchases involves adding a percentage to the original price.
- Tips: Determining a tip at a restaurant involves calculating a percentage of the total bill.
- Interest Rates: Understanding interest rates on loans and savings accounts requires a thorough grasp of percentage calculations.
- Investment Returns: Tracking investment performance involves calculating percentage gains or losses.
- Data Analysis: Percentages are frequently used in data analysis and statistical reports to represent proportions and changes.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The more you practice, the more comfortable you'll become with percentage calculations.
- Use a Calculator: For complex calculations, using a calculator ensures accuracy.
- Break Down Complex Problems: If a problem seems overwhelming, break it down into smaller, manageable steps.
- Check Your Work: Always double-check your calculations to avoid errors.
- Understand the Concept: Focus on understanding the underlying principles of percentages, not just memorizing formulas.
Conclusion: Unlocking the Power of Percentages
The seemingly simple question, "What is 20% off of 300?" opens up a world of practical applications for percentage calculations. Mastering this skill empowers you to make informed financial decisions, analyze data effectively, and navigate various real-life scenarios confidently. Whether you choose the decimal, fraction, or complement method, the key is understanding the principles and applying them consistently. By practicing regularly and using the appropriate tools, you can unlock the power of percentages and enhance your numerical literacy. Remember, the ability to perform these calculations accurately is a valuable asset in today's world.
Latest Posts
Latest Posts
-
What Is Worse For Liver Sugar Or Alcohol
Jun 05, 2025
-
How To Regulate Period On Spironolactone
Jun 05, 2025
-
Can Thc Be Absorbed Through Skin
Jun 05, 2025
-
Compared Human Full Grown Earless Monitor Lizard
Jun 05, 2025
-
Can Dogs Get Rotavirus From Humans
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Off Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.