What Is 2 To The Power Of 1
listenit
May 24, 2025 · 6 min read
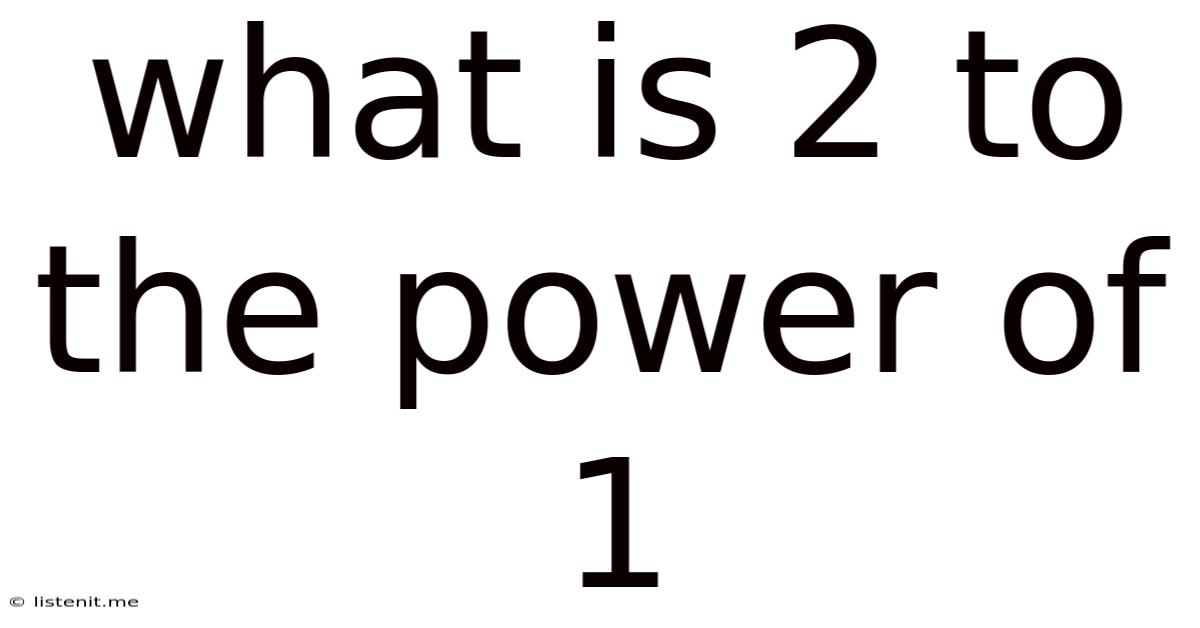
Table of Contents
What is 2 to the Power of 1? A Deep Dive into Exponentiation
The seemingly simple question, "What is 2 to the power of 1?" might appear trivial at first glance. However, understanding this seemingly basic concept unlocks a deeper understanding of exponentiation, a fundamental operation in mathematics with far-reaching implications in various fields, from simple arithmetic to complex scientific calculations and computer science. This article will explore this seemingly simple equation, delving into the mechanics of exponentiation, its applications, and its significance in the broader mathematical landscape.
Understanding Exponentiation: The Fundamentals
Exponentiation, at its core, represents repeated multiplication. When we write a number as b<sup>n</sup>, we're essentially saying that we're multiplying the base (b) by itself n times. The number n is called the exponent or power, while b is the base.
So, what does 2<sup>1</sup> mean? Following the definition, it means we multiply the base (2) by itself 1 time. Therefore, 2<sup>1</sup> = 2. It's as straightforward as it seems.
Exploring Different Exponents: A Comparative Analysis
To gain a clearer perspective on 2<sup>1</sup>, let's compare it to other exponents involving the base 2:
- 2<sup>0</sup>: Any number raised to the power of zero equals 1. This is a crucial rule in exponentiation. Thus, 2<sup>0</sup> = 1.
- 2<sup>1</sup>: As we've established, 2<sup>1</sup> = 2. This represents the base itself, a single instance of the number.
- 2<sup>2</sup>: This means 2 multiplied by itself twice: 2 x 2 = 4.
- 2<sup>3</sup>: This is 2 multiplied by itself three times: 2 x 2 x 2 = 8.
- 2<sup>4</sup>: This is 2 multiplied by itself four times: 2 x 2 x 2 x 2 = 16.
- 2<sup>-1</sup>: Negative exponents represent reciprocals. 2<sup>-1</sup> = 1/2 = 0.5.
- 2<sup>-2</sup>: This is the reciprocal of 2<sup>2</sup>: 1/(2 x 2) = 1/4 = 0.25.
This pattern demonstrates how the value of the expression grows as the exponent increases. Understanding this progression helps contextualize the significance of 2<sup>1</sup> as the foundational step in this exponential growth.
The Significance of 2<sup>1</sup>: More Than Just a Simple Calculation
While the calculation itself is trivial, the significance of 2<sup>1</sup> lies in its role as the building block of exponential functions and its connection to other mathematical concepts.
2<sup>1</sup> as the Identity Element
In mathematics, an identity element is a value that, when combined with another value using a particular operation, leaves the other value unchanged. For multiplication, the identity element is 1. When we multiply any number by 1, the number remains unchanged. In the context of exponentiation, we can think of 2<sup>1</sup> as representing the "identity" of the base 2 within the realm of exponentiation.
Applications in Computer Science: Binary Numbers and Boolean Logic
The number 2 plays a pivotal role in computer science, particularly in binary systems. Binary numbers utilize only two digits, 0 and 1, to represent all numerical values. This system is fundamental to how computers store and process information. The exponent 1, in this context, signifies the presence of a single digit (1) in a particular binary position. For example, the binary number 10 (which is 2 in decimal) can be interpreted as 1 x 2<sup>1</sup> + 0 x 2<sup>0</sup>. Understanding the impact of the exponent '1' here is key to comprehending how binary numbers work.
Applications in Exponential Growth and Decay
Exponential functions are ubiquitous in modeling real-world phenomena involving growth or decay. Population growth, compound interest, radioactive decay—these processes often exhibit exponential behavior. The simplest exponential function, f(x) = 2<sup>x</sup>, starts with the value 2<sup>1</sup> = 2 when x = 1, forming the base for further exponential growth. Understanding the foundational element of 2<sup>1</sup> is crucial to grasping the underlying principles of these processes.
Beyond the Basics: Exploring Related Concepts
Understanding 2<sup>1</sup> opens doors to exploring more complex aspects of mathematics:
Logarithms: The Inverse of Exponentiation
Logarithms are the inverse operation of exponentiation. If 2<sup>x</sup> = y, then log<sub>2</sub>(y) = x. The logarithm base 2 of y is the exponent to which 2 must be raised to obtain y. Understanding the relationship between exponents and logarithms is crucial for solving many mathematical problems. The simple case of 2<sup>1</sup> = 2 translates directly to log<sub>2</sub>(2) = 1.
Complex Numbers and Exponentiation
Exponentiation can be extended to complex numbers, which involve imaginary units (√-1 denoted as 'i'). The power of 1 applied to a complex number leaves the complex number unchanged. While the calculations become more involved, the fundamental principle of exponentiation remains consistent.
Calculus and Exponential Functions
In calculus, exponential functions are differentiable and integrable. Their derivatives and integrals are directly related to the original exponential function, highlighting their unique mathematical properties. The simple case of 2<sup>1</sup> serves as a starting point for understanding the behavior of these functions and their derivatives and integrals.
Practical Applications: Real-World Examples
The concept of 2<sup>1</sup>, despite its simplicity, finds practical applications in numerous fields:
- Finance: Calculating simple interest involves understanding exponential growth; 2<sup>1</sup> forms a crucial part of this.
- Engineering: Many engineering problems involve exponential models. The fundamental understanding of exponentiation, starting with the simplest example like 2<sup>1</sup>, is essential for these calculations.
- Biology: Population growth models often employ exponential functions.
- Physics: Radioactive decay follows an exponential pattern, with the foundational concept being the power operation which has 2<sup>1</sup> as one of its most basic cases.
Conclusion: The Unsung Importance of a Simple Equation
The equation 2<sup>1</sup> = 2 might seem insignificant at first. However, its simplicity belies its profound importance. It serves as the fundamental building block for understanding exponentiation, a core concept in mathematics with widespread applications in diverse fields. From the binary system of computers to the modeling of exponential growth and decay in the natural world, the principles underlying 2<sup>1</sup> underpin much of our quantitative understanding of the world. Mastering this simple concept provides a solid foundation for tackling more complex mathematical challenges and understanding the intricate processes that govern our universe. Its seemingly simple nature should not detract from its critical role in the broader mathematical landscape. The seemingly trivial case of 2 raised to the power of 1 represents much more than just a simple arithmetic calculation—it is a keystone to unlocking a more profound understanding of mathematics and its applications.
Latest Posts
Latest Posts
-
15 Out Of 22 As A Percentage
May 24, 2025
-
Do I Have An Hourglass Shape
May 24, 2025
-
What Was 21 Years Ago Today
May 24, 2025
-
6 Months From September 1 2023
May 24, 2025
-
What Is Half Of 17 And 3 4
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 To The Power Of 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.