What Is 2 Root 3 Squared
listenit
May 10, 2025 · 4 min read
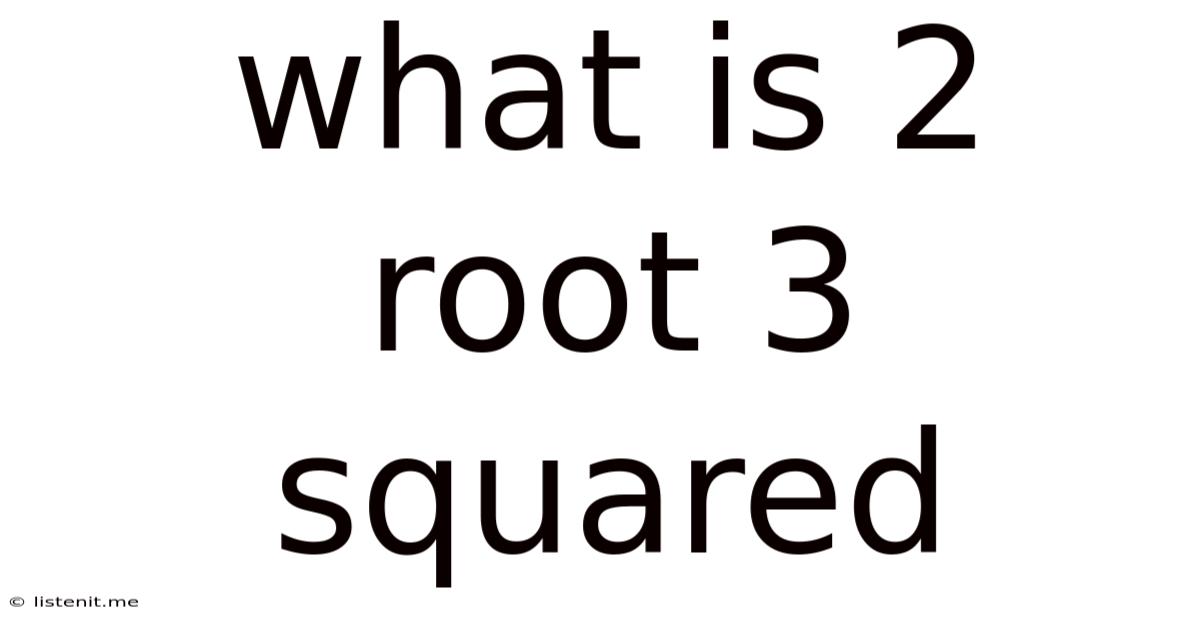
Table of Contents
What is 2√3 Squared? A Comprehensive Exploration
Understanding the squaring of surds, particularly expressions like (2√3)², is fundamental in algebra and various mathematical applications. This article delves deep into this concept, explaining not just the answer but the underlying principles and broader implications. We’ll explore the process step-by-step, discuss related concepts like simplifying square roots and expanding brackets, and even touch on practical applications of this seemingly simple calculation.
Understanding the Basics: Squaring a Number
Before tackling (2√3)², let's refresh our understanding of squaring. Squaring a number means multiplying it by itself. For example:
- 2² = 2 × 2 = 4
- 5² = 5 × 5 = 25
- 10² = 10 × 10 = 100
This principle applies equally to expressions involving surds (numbers containing square roots).
Deconstructing (2√3)²: A Step-by-Step Approach
Now, let's break down the calculation of (2√3)²:
(2√3)² = (2√3) × (2√3)
This is simply applying the definition of squaring. Now, we can use the distributive property of multiplication (often referred to as the FOIL method when expanding brackets):
(2√3) × (2√3) = 2 × 2 × √3 × √3
This simplifies to:
4 × √9
Since the square root of 9 is 3, we get:
4 × 3 = 12
Therefore, (2√3)² = 12.
Why This Works: The Power of Indices
The solution above utilizes the fundamental rules of indices. Specifically, we employed the following rule:
(ab)² = a²b²
In our case, a = 2 and b = √3. Substituting these values, we get:
(2√3)² = 2² × (√3)² = 4 × 3 = 12
This demonstrates the power of understanding index laws in simplifying mathematical expressions. This method is more efficient and applicable to more complex expressions than directly expanding the brackets.
Simplifying Square Roots: A Crucial Skill
The ability to simplify square roots is crucial for solving problems involving surds. Consider this example:
√75
To simplify this, we look for perfect square factors of 75. Since 75 = 25 × 3, and 25 is a perfect square (5²), we can rewrite the expression as:
√(25 × 3) = √25 × √3 = 5√3
This simplification is vital when working with more complex surd expressions. Mastering this skill will significantly enhance your ability to solve a wide range of algebraic problems.
Expanding Brackets: Another Essential Technique
Expanding brackets (using the distributive property) is another key algebraic skill. It helps in simplifying expressions like:
(a + b)(c + d) = ac + ad + bc + bd
In our initial problem, we used a simplified version of this:
(2√3)(2√3) = 2 × 2 × √3 × √3 = 4 × 3 = 12
The ability to expand brackets correctly is crucial for more complicated expressions involving surds and other algebraic terms.
Beyond the Basics: Applications of Squaring Surds
The concept of squaring surds isn't just an abstract mathematical exercise. It has practical applications in various fields:
1. Geometry and Trigonometry
Calculations involving areas and lengths of triangles often involve surds. For instance, finding the area of an equilateral triangle with side length 'x' requires squaring surds.
2. Physics
Many physics formulas, particularly those dealing with vectors and motion, involve square roots and squaring. Understanding how to manipulate surds is therefore crucial for solving physics problems accurately.
3. Engineering
Engineering designs often incorporate calculations that involve surds, especially in areas like structural analysis and fluid dynamics.
4. Computer Graphics
In computer graphics, manipulating surds is important for calculations relating to transformations, rotations, and scaling of images.
Further Exploration: More Complex Surd Expressions
Let's consider slightly more complex scenarios:
(3√2 + 4)²
To solve this, we use the formula for expanding brackets (a + b)² = a² + 2ab + b²:
(3√2 + 4)² = (3√2)² + 2(3√2)(4) + 4² = 18 + 24√2 + 16 = 34 + 24√2
(√5 - √2)(√5 + √2)
This example showcases the difference of squares: (a - b)(a + b) = a² - b²:
(√5 - √2)(√5 + √2) = (√5)² - (√2)² = 5 - 2 = 3
These examples highlight the importance of applying different algebraic techniques—such as expanding brackets and the difference of squares—when dealing with more complex expressions involving surds.
Conclusion: Mastering Surds for Mathematical Proficiency
Understanding how to square surds, such as (2√3)², is a fundamental algebraic skill with far-reaching applications. This article provided a step-by-step guide, highlighting the importance of simplifying square roots, expanding brackets, and applying index laws. Mastering these techniques is crucial for tackling more complex mathematical problems in various fields, from geometry and trigonometry to physics and engineering. Remember to practice regularly to solidify your understanding and build confidence in handling surds effectively. The more you practice, the more intuitive these manipulations will become. From simple calculations to complex algebraic expressions, a solid grasp of surd manipulation is key to mathematical proficiency.
Latest Posts
Latest Posts
-
1 And 7 8 As An Improper Fraction
May 10, 2025
-
Which Missing Item Would Complete This Beta Decay Reaction
May 10, 2025
-
What Is The Oxidation Number Of Fe In Fe2o3
May 10, 2025
-
How To Calculate Second Ionization Energy
May 10, 2025
-
How Many Valence Electrons Do All Alkali Metals Have
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 Root 3 Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.