What Is 2 Divided By 1/5
listenit
May 24, 2025 · 5 min read
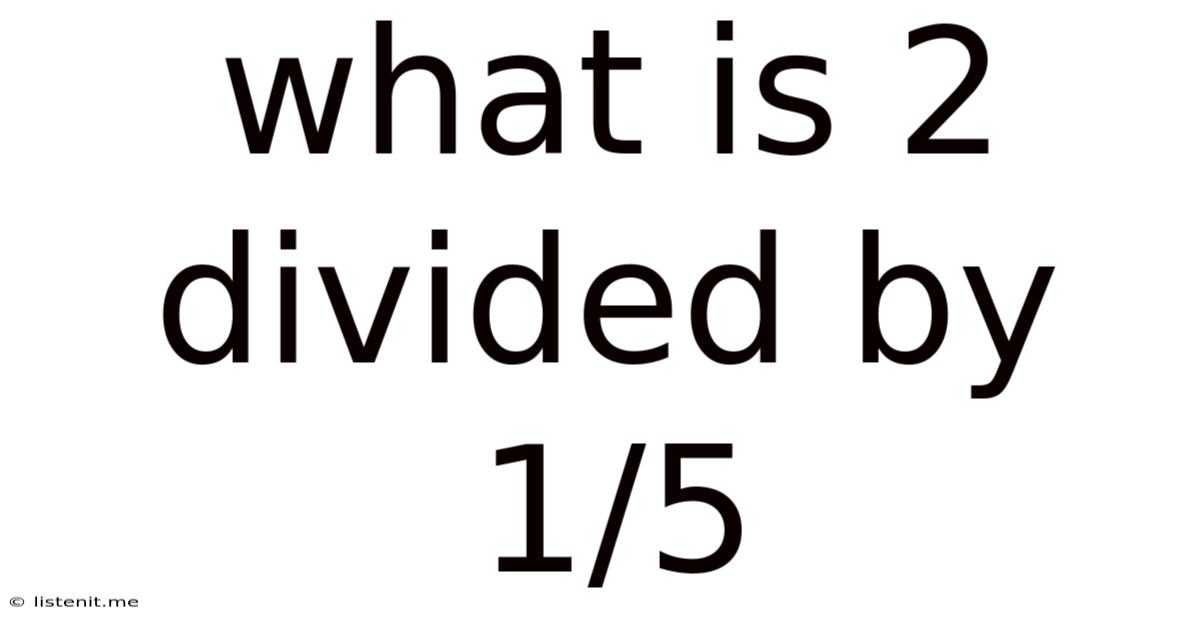
Table of Contents
What is 2 Divided by 1/5? A Deep Dive into Fraction Division
The seemingly simple question, "What is 2 divided by 1/5?" often trips up students and adults alike. While the answer itself is straightforward, understanding the underlying principles of fraction division is crucial for mastering more complex mathematical concepts. This article will not only provide the solution but also explore the "why" behind the process, offering various methods to tackle similar problems and highlighting the importance of conceptual understanding in mathematics.
Understanding Fraction Division: The Basics
Before diving into the specific problem, let's establish a foundational understanding of fraction division. Dividing by a fraction is essentially the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/5 is 5/1 (or simply 5).
This principle stems from the definition of division. When we divide a number (a) by another number (b), we're essentially asking, "How many times does b fit into a?" Applying this to fractions, dividing 2 by 1/5 asks, "How many times does 1/5 fit into 2?"
This visual representation helps solidify the concept. Imagine a pizza cut into 5 slices. Each slice represents 1/5 of the pizza. If you have two whole pizzas, you can see that you have ten (2 x 5) slices of 1/5 each.
Method 1: The Reciprocal Method
This is the most common and efficient method for dividing by a fraction. The steps are simple:
-
Find the reciprocal of the divisor: The divisor is the fraction you're dividing by (in this case, 1/5). Its reciprocal is 5/1, or 5.
-
Change the division to multiplication: Replace the division symbol (÷) with a multiplication symbol (×).
-
Multiply the numerators: Multiply the numerator of the first number (2, which can be written as 2/1) by the numerator of the reciprocal (5). 2 x 5 = 10
-
Multiply the denominators: Multiply the denominator of the first number (1) by the denominator of the reciprocal (1). 1 x 1 = 1
-
Simplify the result: The resulting fraction is 10/1, which simplifies to 10.
Therefore, 2 divided by 1/5 is 10.
Method 2: The Common Denominator Method
This method is less efficient for simple problems but provides a stronger conceptual understanding, particularly for those struggling with the reciprocal method.
-
Convert the whole number to a fraction: Express 2 as a fraction: 2/1.
-
Find a common denominator: Find a common denominator for both fractions. In this case, the common denominator is 5.
-
Rewrite the fractions with the common denominator: 2/1 becomes 10/5 (by multiplying both numerator and denominator by 5).
-
Divide the numerators: Divide the numerator of the first fraction (10) by the numerator of the second fraction (1). 10 ÷ 1 = 10
-
Keep the denominator: The denominator remains the same (5).
-
Simplify (if needed): The result is 10/5, which simplifies to 10.
This method reinforces the idea of division as finding how many times one fraction fits into another. We've essentially asked, "How many 1/5s are there in 10/5?"
Method 3: Visual Representation
Visualizing the problem can be incredibly helpful, especially for beginners. Consider using diagrams or manipulatives.
Imagine you have two whole objects (pizzas, cakes, etc.). Each object is divided into five equal parts. How many total parts (1/5s) do you have? Counting them will reveal 10 parts, reiterating that 2 divided by 1/5 equals 10.
Real-World Applications of Fraction Division
Understanding fraction division isn't just an academic exercise; it has numerous practical applications in everyday life. Here are a few examples:
-
Cooking and Baking: Many recipes require precise measurements. If a recipe calls for 1/5 cup of sugar and you want to double the recipe, you'll need to calculate 2 divided by 1/5 to find the total amount of sugar required.
-
Sewing and Crafts: Calculating fabric requirements for projects often involves fractions. Dividing a larger length of fabric by the length needed for individual pieces frequently requires fraction division.
-
Construction and Engineering: Precise measurements are crucial in construction. Calculating the number of smaller units (e.g., bricks or tiles) needed for a larger area often necessitates fraction division.
-
Finance and Budgeting: Dividing a budget across various categories frequently involves fractions and decimals. Understanding fraction division is crucial for accurate budget allocation.
Tackling More Complex Problems
The principles outlined above can be extended to more complex fraction division problems. For instance, consider the problem: 3/4 divided by 2/5. We would follow the same steps:
-
Find the reciprocal: The reciprocal of 2/5 is 5/2.
-
Change to multiplication: 3/4 ÷ 2/5 becomes 3/4 × 5/2.
-
Multiply numerators and denominators: (3 x 5) / (4 x 2) = 15/8.
-
Simplify (if needed): The fraction 15/8 can be simplified to 1 and 7/8 or 1.875.
Common Mistakes to Avoid
Several common errors can occur when performing fraction division:
-
Forgetting to find the reciprocal: This is the most common mistake. Remember, you're not simply multiplying the fractions; you're multiplying the first fraction by the reciprocal of the second.
-
Incorrectly multiplying or simplifying: Carefully multiply the numerators and denominators and ensure the final fraction is simplified to its lowest terms.
-
Misunderstanding the concept of reciprocals: Ensure you have a firm grasp on what a reciprocal is and how to find it.
Conclusion: Mastering Fraction Division
The seemingly simple question, "What is 2 divided by 1/5?" opens a door to a broader understanding of fraction division. By mastering the reciprocal method, common denominator method, and visual representation techniques, you can confidently tackle various fraction division problems. Remember to practice regularly, focusing on understanding the underlying principles rather than simply memorizing steps. This approach will build a strong mathematical foundation, paving the way for success in more advanced mathematical concepts. The ability to confidently work with fractions is a valuable skill with widespread applications in various aspects of life, making its mastery a worthwhile investment of time and effort.
Latest Posts
Latest Posts
-
What Grade Is 60 Percent Out Of 100
May 24, 2025
-
What Is The Least Common Multiple Of 24 And 32
May 24, 2025
-
Greatest Common Factors Of 8 And 12
May 24, 2025
-
30 Days After August 22 2024
May 24, 2025
-
What Is 6 Divided By 7
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 Divided By 1/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.