What Is 2.5 As A Percent
listenit
Mar 21, 2025 · 4 min read
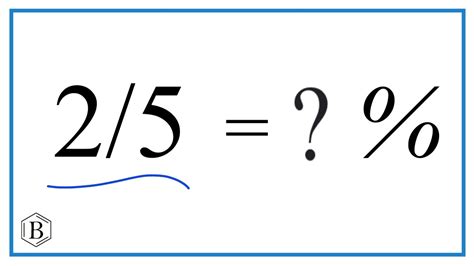
Table of Contents
What is 2.5 as a Percent? A Comprehensive Guide
Understanding how to convert decimals to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to interpreting statistical data and analyzing financial reports. This comprehensive guide delves into the process of converting 2.5 to a percentage, explaining the underlying concepts and providing various approaches to solve this and similar problems. We'll also explore the broader context of decimal-to-percentage conversions and their real-world implications.
Understanding Percentages
Before we dive into converting 2.5, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of a hundred." Therefore, 25% means 25 out of 100, or 25/100, which simplifies to 1/4.
This fundamental understanding forms the basis for all percentage calculations. Any fraction, decimal, or ratio can be expressed as a percentage, providing a standardized way to compare and interpret different quantities.
Method 1: The Direct Conversion Method
The most straightforward way to convert 2.5 to a percentage is to multiply the decimal by 100. This is because percentages represent parts of 100.
Step 1: Multiply by 100
2.5 * 100 = 250
Step 2: Add the Percentage Symbol
250%
Therefore, 2.5 as a percentage is 250%.
Method 2: The Fractional Method
This method involves expressing the decimal as a fraction and then converting the fraction to a percentage.
Step 1: Express as a Fraction
2.5 can be written as the improper fraction 25/10. (Remember, the decimal point signifies the tenths place, so 2.5 is the same as 2 and 5/10)
Step 2: Convert to an Equivalent Fraction with a Denominator of 100
To convert to a percentage, we need a denominator of 100. To achieve this, we can multiply both the numerator and denominator by 10:
(25/10) * (10/10) = 250/100
Step 3: Express as a Percentage
Since a percentage is a fraction out of 100, 250/100 is equivalent to 250%.
Method 3: Using Proportions
This method uses the concept of proportion to solve for the percentage.
Step 1: Set up a Proportion
We can set up a proportion where x represents the percentage we're trying to find:
2.5 / 1 = x / 100
Step 2: Solve for x
Cross-multiply:
2.5 * 100 = 1 * x
250 = x
Therefore, x = 250%.
Understanding the Result: What does 250% mean?
It's crucial to understand what 250% represents. A percentage greater than 100% signifies a value that exceeds the whole. In this case, 250% means 2.5 times the original whole. For example, if you had 100 apples and increased that amount by 250%, you'd now have 350 apples (100 + 250% of 100 = 100 + 250 = 350).
Practical Applications of Decimal-to-Percentage Conversions
The ability to convert decimals to percentages is invaluable in numerous real-world scenarios:
- Finance: Calculating interest rates, returns on investment, and changes in stock prices.
- Retail: Determining discounts, sales tax, and profit margins.
- Statistics: Interpreting data, such as survey results and population growth rates.
- Science: Representing experimental data and analyzing scientific measurements.
- Everyday Life: Calculating tips, splitting bills, and understanding proportions in recipes.
Beyond 2.5: Converting Other Decimals to Percentages
The methods outlined above can be applied to convert any decimal to a percentage. Simply follow the steps:
- Multiply the decimal by 100.
- Add the percentage symbol (%).
Examples:
- 0.75 = 0.75 * 100 = 75%
- 0.05 = 0.05 * 100 = 5%
- 1.2 = 1.2 * 100 = 120%
- 3.14 = 3.14 * 100 = 314%
Common Mistakes to Avoid
While the conversion process itself is relatively simple, some common mistakes can occur:
- Forgetting to multiply by 100: This is the most frequent error. Remember that percentages are always expressed out of 100.
- Incorrect placement of the decimal point: Ensure the decimal point is correctly placed before multiplying by 100.
- Misinterpreting percentages greater than 100%: Remember that these percentages represent values exceeding the original whole.
Conclusion
Converting 2.5 to a percentage, resulting in 250%, is a straightforward process achievable using various methods. Understanding this fundamental conversion is key to navigating numerous aspects of daily life, from personal finance to professional applications. By mastering this skill and avoiding common errors, you'll be well-equipped to handle a wide range of percentage calculations with confidence. Remember that the ability to confidently work with percentages significantly enhances your mathematical literacy and problem-solving abilities. Practice consistently, explore different methods, and always strive for a clear understanding of the underlying principles to solidify your expertise.
Latest Posts
Latest Posts
-
Do Protists Make Their Own Food
May 09, 2025
-
38 Out Of 60 As A Percentage
May 09, 2025
-
How Many Ounces Are In 1 05 Qt
May 09, 2025
-
How To Determine Most Stable Chair Conformation
May 09, 2025
-
A Pair Of Pants With A Marked Price Of 35 00
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 2.5 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.