What Is 2 3 Of 20
listenit
May 21, 2025 · 4 min read
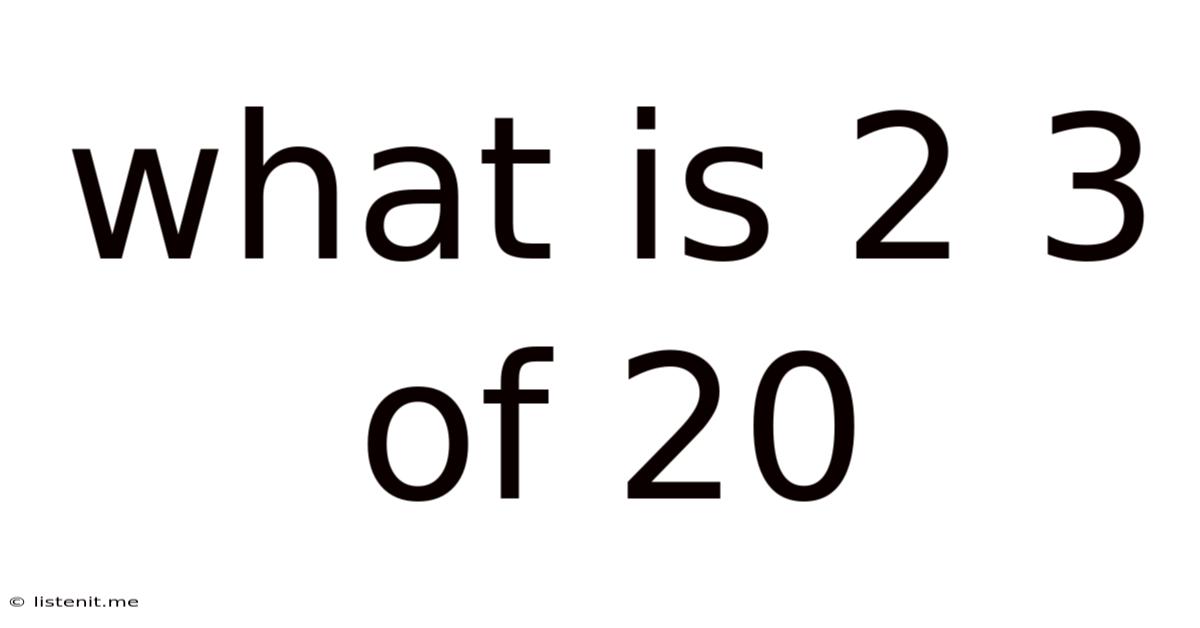
Table of Contents
What is 2/3 of 20? A Comprehensive Guide to Fractions and Percentage Calculations
Finding a fraction of a number is a fundamental mathematical concept with broad applications in everyday life, from calculating discounts and sales tax to understanding proportions in recipes and determining project progress. This article delves into the question, "What is 2/3 of 20?", providing a detailed explanation of the calculation process, exploring various approaches, and highlighting the practical significance of understanding fractions and percentages.
Understanding the Problem: 2/3 of 20
The phrase "2/3 of 20" signifies the need to find two-thirds of the quantity 20. This involves determining a fractional part of a whole number. Let's break down the problem step-by-step, using multiple methods to reinforce the concept.
Method 1: Direct Multiplication
The most straightforward method involves multiplying the fraction (2/3) by the whole number (20).
-
Step 1: Convert the whole number into a fraction: We can represent 20 as a fraction by placing it over 1: 20/1.
-
Step 2: Multiply the numerators and denominators: Multiply the numerators (top numbers) together and the denominators (bottom numbers) together.
(2/3) * (20/1) = (2 * 20) / (3 * 1) = 40/3
-
Step 3: Simplify the fraction: The resulting fraction, 40/3, is an improper fraction (the numerator is larger than the denominator). To simplify, we perform division.
40 ÷ 3 = 13 with a remainder of 1
-
Step 4: Express the result: The result can be expressed as a mixed number (a whole number and a fraction): 13 1/3
Therefore, 2/3 of 20 is 13 1/3.
Method 2: Finding One-Third, then Doubling
This method breaks the problem into smaller, more manageable steps.
-
Step 1: Find one-third of 20: Divide 20 by 3: 20 ÷ 3 = 6.666... (approximately 6.67)
-
Step 2: Double the result: Since we need two-thirds, we multiply the result from Step 1 by 2: 6.666... * 2 = 13.333... (approximately 13.33)
This method also arrives at approximately 13.33, which is the decimal equivalent of 13 1/3.
Method 3: Using Decimal Equivalents
This method involves converting the fraction to its decimal equivalent before performing the calculation.
-
Step 1: Convert the fraction to a decimal: Divide the numerator by the denominator: 2 ÷ 3 ≈ 0.6667
-
Step 2: Multiply the decimal by the whole number: Multiply the decimal equivalent by 20: 0.6667 * 20 ≈ 13.334
Again, we arrive at approximately 13.33, confirming the previous results.
Understanding the Significance of the Result
The result, 13 1/3, highlights the importance of understanding fractions and their representation. While the decimal approximation (13.33) is useful in certain contexts, the fractional representation (13 1/3) is more precise and avoids rounding errors. This precision is crucial in various applications:
Real-World Applications of Fractional Calculations:
-
Cooking and Baking: Recipes often involve fractional measurements (e.g., 2/3 cup of flour). Accurately calculating these fractions ensures consistent results.
-
Construction and Engineering: Precise measurements are critical in construction and engineering projects. Fractions play a crucial role in ensuring accuracy and preventing errors.
-
Finance and Budgeting: Calculating percentages (which are essentially fractions) is vital for managing personal finances, understanding interest rates, and calculating discounts and sales tax.
-
Data Analysis and Statistics: Fractions and percentages are frequently used in analyzing data, representing proportions, and interpreting statistical results.
-
Project Management: Tracking project progress often involves representing completed tasks as fractions of the total project.
Expanding the Concept: Percentages and Proportions
The concept of "2/3 of 20" can be further extended to explore percentages and proportions.
-
Converting Fractions to Percentages: To express 2/3 as a percentage, we multiply it by 100%: (2/3) * 100% ≈ 66.67%
-
Understanding Proportions: The calculation illustrates a proportional relationship. If 2/3 of 20 is 13 1/3, then 1/3 of 20 is approximately 6.67. This proportional relationship allows us to scale the calculation for different fractions of 20.
Advanced Applications and Problem Solving:
The principles demonstrated in solving "2/3 of 20" are fundamental to more complex mathematical problems, including:
-
Solving equations involving fractions: Understanding fraction manipulation is crucial for solving algebraic equations that contain fractions.
-
Working with ratios and proportions: Many real-world problems involve ratios and proportions, and the ability to work with fractions is essential for solving these problems.
-
Calculating compound interest: Understanding compound interest calculations relies heavily on the ability to work with fractions and percentages.
Conclusion: Mastering Fractions and Their Applications
Mastering the ability to calculate fractions, such as finding "2/3 of 20," is a crucial skill applicable across numerous fields. By understanding the different methods of calculation and appreciating the precision of fractional representation, we can confidently tackle various mathematical challenges and apply these skills to real-world situations. The ability to work fluently with fractions forms a cornerstone of mathematical literacy and empowers us to solve practical problems effectively. Remember to practice regularly to solidify your understanding and enhance your problem-solving skills. This consistent practice will improve your ability to tackle more complex scenarios confidently.
Latest Posts
Latest Posts
-
The Evolution Of Eukaryotic Cells Most Likely Involved
Jun 05, 2025
-
P Wave Inversion In V1 And V2
Jun 05, 2025
-
Life Expectancy After Distal Pancreatectomy And Splenectomy
Jun 05, 2025
-
Normal X Ray Of Right Foot
Jun 05, 2025
-
Can Drug Use Cause Multiple Sclerosis
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 3 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.