What Is 2 3 Minus 1 4
listenit
May 24, 2025 · 5 min read
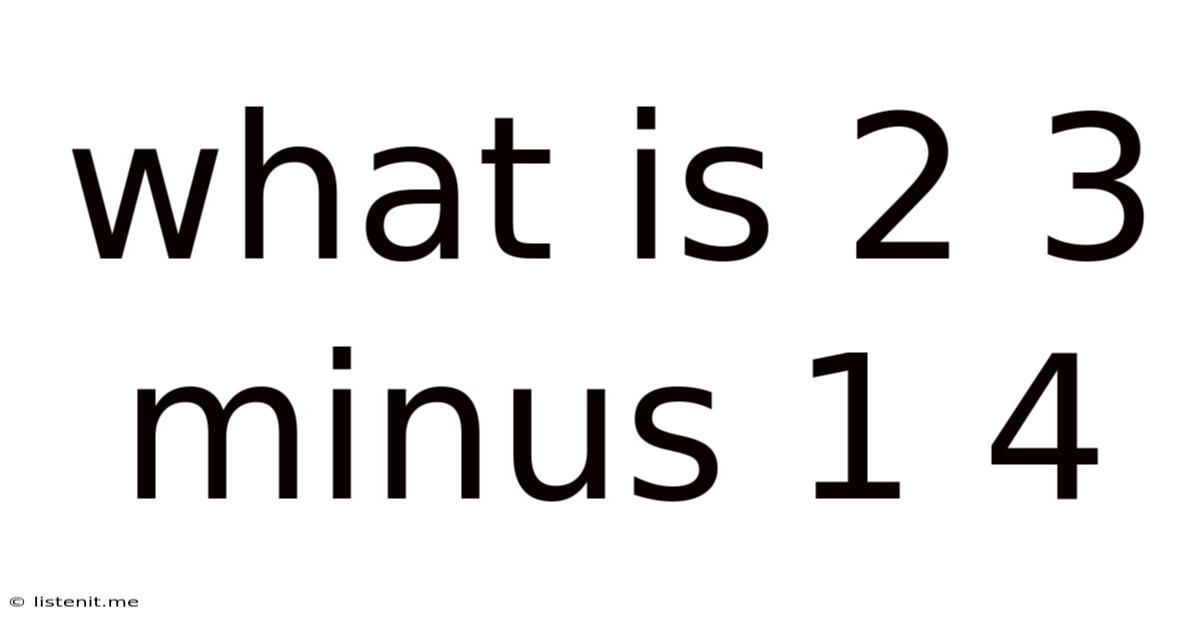
Table of Contents
What is 2/3 Minus 1/4? A Deep Dive into Fraction Subtraction
This seemingly simple question, "What is 2/3 minus 1/4?", opens a door to a world of fundamental mathematical concepts. While the answer itself is straightforward, understanding the process of subtracting fractions reveals crucial skills applicable across various mathematical fields. This article will not only provide the solution but will also explore the underlying principles, offering a comprehensive guide suitable for students, educators, and anyone looking to refresh their knowledge of fractions.
Understanding Fractions: A Foundation for Subtraction
Before tackling the subtraction, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator indicates how many of those parts we're considering.
For example, in the fraction 2/3, the denominator (3) means the whole is divided into three equal parts, and the numerator (2) means we're considering two of those parts.
Key Concepts for Fraction Subtraction
Subtracting fractions requires a critical understanding of a few key concepts:
-
Common Denominator: This is the cornerstone of fraction subtraction. Before we can subtract fractions, their denominators must be the same. Think of it like comparing apples to apples – you can't directly subtract apples from oranges.
-
Equivalent Fractions: These are fractions that represent the same value, even though they look different. For example, 1/2 is equivalent to 2/4, 3/6, 4/8, and so on. Finding equivalent fractions with a common denominator is essential for subtraction.
-
Simplifying Fractions: Once you've performed the subtraction, you often need to simplify the resulting fraction to its lowest terms. This involves dividing both the numerator and the denominator by their greatest common divisor (GCD).
Solving 2/3 - 1/4: A Step-by-Step Approach
Now, let's apply these concepts to solve our problem: 2/3 - 1/4.
Step 1: Find a Common Denominator
The denominators are 3 and 4. To find a common denominator, we look for the least common multiple (LCM) of 3 and 4. The LCM is the smallest number that is a multiple of both 3 and 4. In this case, the LCM of 3 and 4 is 12.
Step 2: Convert Fractions to Equivalent Fractions with the Common Denominator
We need to convert both 2/3 and 1/4 into equivalent fractions with a denominator of 12.
-
For 2/3: To change the denominator from 3 to 12, we multiply by 4 (12/3 = 4). To maintain the value of the fraction, we must multiply both the numerator and the denominator by 4: (2 x 4) / (3 x 4) = 8/12.
-
For 1/4: To change the denominator from 4 to 12, we multiply by 3 (12/4 = 3). Again, we multiply both the numerator and the denominator by 3: (1 x 3) / (4 x 3) = 3/12.
Step 3: Perform the Subtraction
Now that both fractions have the same denominator, we can subtract the numerators:
8/12 - 3/12 = (8 - 3) / 12 = 5/12
Step 4: Simplify the Result (If Necessary)
In this case, the fraction 5/12 is already in its simplest form. The greatest common divisor of 5 and 12 is 1, meaning there are no common factors to divide both the numerator and denominator by.
Therefore, 2/3 - 1/4 = 5/12
Visualizing Fraction Subtraction: A Concrete Approach
Understanding fractions can be enhanced through visualization. Imagine a pizza cut into 12 slices.
- 2/3 of the pizza would be 8 slices (8/12).
- 1/4 of the pizza would be 3 slices (3/12).
- Subtracting 1/4 from 2/3 leaves you with 5 slices, representing 5/12 of the pizza.
Beyond the Basics: More Complex Fraction Subtraction
The principles we've covered apply to more complex scenarios. Let's consider some examples:
Subtracting Mixed Numbers
A mixed number combines a whole number and a fraction (e.g., 1 1/2). To subtract mixed numbers, you can either convert them to improper fractions (where the numerator is larger than the denominator) or subtract the whole numbers and fractions separately.
Example: 2 1/3 - 1 1/4
- Convert to Improper Fractions: 2 1/3 = 7/3 and 1 1/4 = 5/4.
- Find a Common Denominator: The LCM of 3 and 4 is 12.
- Convert to Equivalent Fractions: 7/3 = 28/12 and 5/4 = 15/12.
- Subtract: 28/12 - 15/12 = 13/12.
- Convert back to a Mixed Number (if necessary): 13/12 = 1 1/12
Subtracting Fractions with Unlike Denominators and Larger Numbers
The process remains the same, even with larger numbers: find the common denominator, convert to equivalent fractions, subtract the numerators, and simplify. Finding the LCM for larger numbers might require prime factorization or other techniques.
Applications of Fraction Subtraction in Real Life
Fraction subtraction is far from a purely academic exercise; it has many practical applications in everyday life:
-
Cooking and Baking: Adjusting recipes, measuring ingredients, and determining leftover portions all involve fraction subtraction.
-
Construction and Engineering: Precise measurements and calculations in construction rely heavily on fractions.
-
Finance and Budgeting: Managing expenses, calculating discounts, and determining savings involve subtracting fractional amounts.
-
Data Analysis: Representing and analyzing data often involves working with fractions and proportions.
-
Time Management: Dividing and allocating time efficiently necessitates working with fractions of hours or minutes.
Conclusion: Mastering Fraction Subtraction
Understanding fraction subtraction is a cornerstone of mathematical proficiency. By mastering the concepts of common denominators, equivalent fractions, and simplification, you equip yourself with a powerful tool applicable across various fields. Whether it's baking a cake, solving an engineering problem, or managing your finances, the ability to confidently subtract fractions is a valuable skill that enhances problem-solving capabilities and promotes a deeper understanding of the mathematical world. The seemingly simple equation, 2/3 - 1/4 = 5/12, encapsulates a wealth of mathematical knowledge and practical utility.
Latest Posts
Latest Posts
-
How Long Was 12 Years Ago
May 24, 2025
-
Born In September 1996 How Old Are You
May 24, 2025
-
Highest Common Factor Of 4 And 8
May 24, 2025
-
How Long Was 17 Years Ago
May 24, 2025
-
7 8 Divided By 2 As A Fraction
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 3 Minus 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.