What Is 2 3 Minus 1 2
listenit
May 21, 2025 · 5 min read
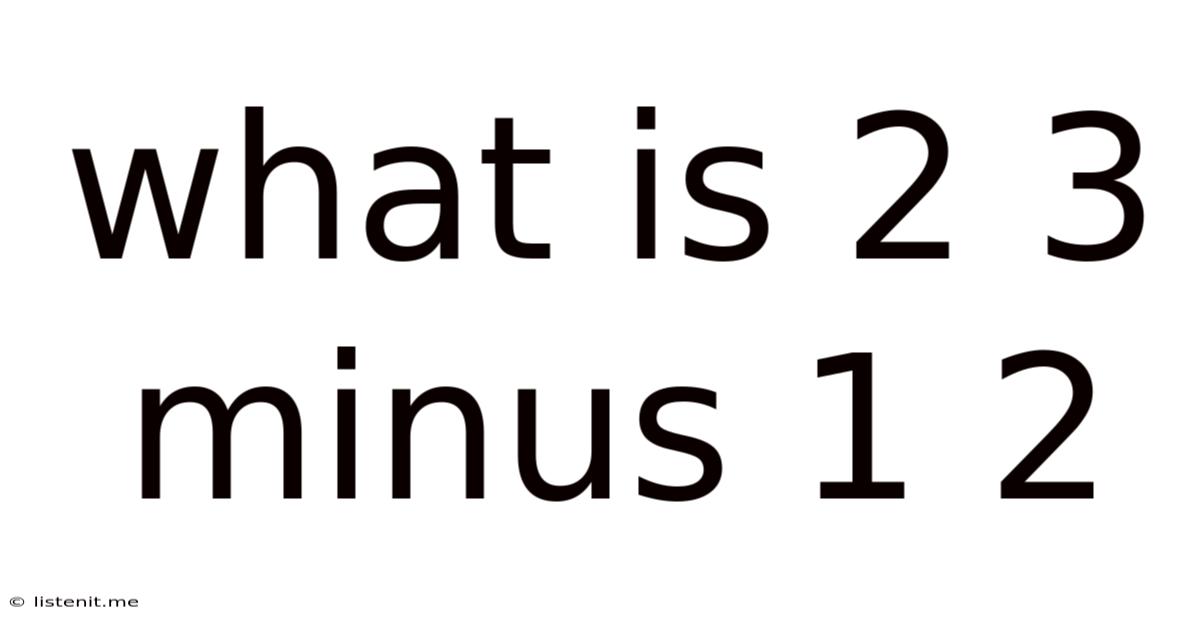
Table of Contents
What is 2/3 Minus 1/2? A Deep Dive into Fraction Subtraction
This seemingly simple question, "What is 2/3 minus 1/2?", opens the door to a fascinating exploration of fundamental arithmetic concepts, particularly fraction subtraction. While the answer itself is straightforward once the method is understood, the underlying principles extend far beyond this single calculation. This article will not only solve the problem but also delve into the 'why' behind the process, offering a comprehensive guide suitable for students and anyone looking to refresh their understanding of fractions. We'll cover different methods, explore related concepts, and even touch upon the practical applications of fraction subtraction in everyday life.
Understanding Fractions: The Building Blocks
Before tackling the subtraction, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number indicates how many parts we have.
- Denominator: The bottom number indicates how many equal parts the whole is divided into.
In our problem, 2/3 has a numerator of 2 and a denominator of 3, meaning we have 2 parts out of a total of 3 equal parts. Similarly, 1/2 represents 1 part out of 2 equal parts.
The Challenge of Unequal Denominators
The core difficulty in subtracting 1/2 from 2/3 lies in the unequal denominators. We cannot directly subtract fractions unless their denominators are the same. Imagine trying to subtract apples from oranges – it's impossible without finding a common unit. The same principle applies to fractions.
Finding the Least Common Denominator (LCD)
To subtract fractions with unequal denominators, we must find their least common denominator (LCD). The LCD is the smallest number that is a multiple of both denominators. For 3 and 2, the multiples are:
- Multiples of 3: 3, 6, 9, 12, 15...
- Multiples of 2: 2, 4, 6, 8, 10...
The smallest number appearing in both lists is 6. Therefore, the LCD of 3 and 2 is 6.
Converting Fractions to a Common Denominator
Now that we have the LCD (6), we need to convert both fractions, 2/3 and 1/2, into equivalent fractions with a denominator of 6. This is done by multiplying both the numerator and the denominator of each fraction by the appropriate factor:
- For 2/3: To get a denominator of 6, we multiply both the numerator and denominator by 2: (2 x 2) / (3 x 2) = 4/6
- For 1/2: To get a denominator of 6, we multiply both the numerator and denominator by 3: (1 x 3) / (2 x 3) = 3/6
Now both fractions have the same denominator, allowing for straightforward subtraction.
Performing the Subtraction
With the fractions converted to a common denominator, we can now perform the subtraction:
4/6 - 3/6 = 1/6
Therefore, 2/3 minus 1/2 equals 1/6.
Visualizing the Subtraction
Visual aids can significantly enhance understanding. Imagine a pizza cut into 6 slices. 2/3 of the pizza would be 4 slices (out of 6). 1/2 of the pizza would be 3 slices (out of 6). Subtracting 3 slices from 4 slices leaves 1 slice, representing 1/6 of the pizza.
Alternative Methods: Using Decimal Representation
While the LCD method is fundamental, we can also solve this problem using decimal representation. Converting the fractions to decimals:
- 2/3 ≈ 0.6667
- 1/2 = 0.5
Subtracting the decimal values:
0.6667 - 0.5 = 0.1667
This decimal, 0.1667, is approximately equal to 1/6. Keep in mind that this method might introduce slight inaccuracies due to rounding, especially when dealing with fractions that don't have exact decimal equivalents (like 2/3).
Expanding the Concept: Subtracting Mixed Numbers
The principles of fraction subtraction extend to mixed numbers (a whole number and a fraction). For example, let's consider subtracting 1 1/2 from 2 2/3.
First, we convert the mixed numbers to improper fractions (where the numerator is larger than the denominator):
- 2 2/3 = (2 x 3 + 2) / 3 = 8/3
- 1 1/2 = (1 x 2 + 1) / 2 = 3/2
Then, we find the LCD of 3 and 2 (which is 6) and convert the fractions:
- 8/3 = (8 x 2) / (3 x 2) = 16/6
- 3/2 = (3 x 3) / (2 x 3) = 9/6
Finally, we subtract:
16/6 - 9/6 = 7/6
This improper fraction can be converted back to a mixed number: 7/6 = 1 1/6
Therefore, 2 2/3 minus 1 1/2 equals 1 1/6.
Real-World Applications of Fraction Subtraction
The seemingly abstract world of fractions finds numerous practical applications in daily life:
- Cooking and Baking: Adjusting recipes, measuring ingredients, and understanding ratios all rely heavily on fraction manipulation.
- Construction and Engineering: Precise measurements and calculations in building and design involve fractions extensively.
- Finance: Dealing with percentages, calculating discounts, and managing budgets often require working with fractions.
- Sewing and Crafting: Accurate fabric measurements and pattern adjustments necessitate a good grasp of fractions.
- Time Management: Dividing time into portions and scheduling tasks often requires understanding fractions of an hour or day.
Conclusion: Mastering Fractions, Mastering Life
Understanding fraction subtraction, while seemingly a basic arithmetic skill, is a cornerstone of mathematical literacy. It's a fundamental skill that extends far beyond the classroom, impacting various aspects of our daily lives. By mastering the concepts of least common denominators, equivalent fractions, and the proper methods of subtraction, we unlock a powerful tool for problem-solving and navigating the quantitative world around us. The simple calculation of 2/3 minus 1/2 serves as a gateway to a deeper appreciation of the elegance and practicality of mathematics. Through diligent practice and a solid understanding of the underlying principles, anyone can confidently conquer fraction subtraction and its many real-world applications. Remember, the key lies in breaking down complex problems into smaller, manageable steps, just as we did in solving this seemingly simple equation.
Latest Posts
Latest Posts
-
Upper Pole Of Kidney On Ultrasound
Jun 05, 2025
-
Giant Cell Tumor Of Bone Histology
Jun 05, 2025
-
Basal Cell Chicken Pox Scar Leg
Jun 05, 2025
-
Lip Lowering Surgery For Gummy Smile
Jun 05, 2025
-
Cpt Code For In Vitro Fertilization
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 3 Minus 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.