What Is 2/3 - 1/4 In Fraction
listenit
May 21, 2025 · 6 min read
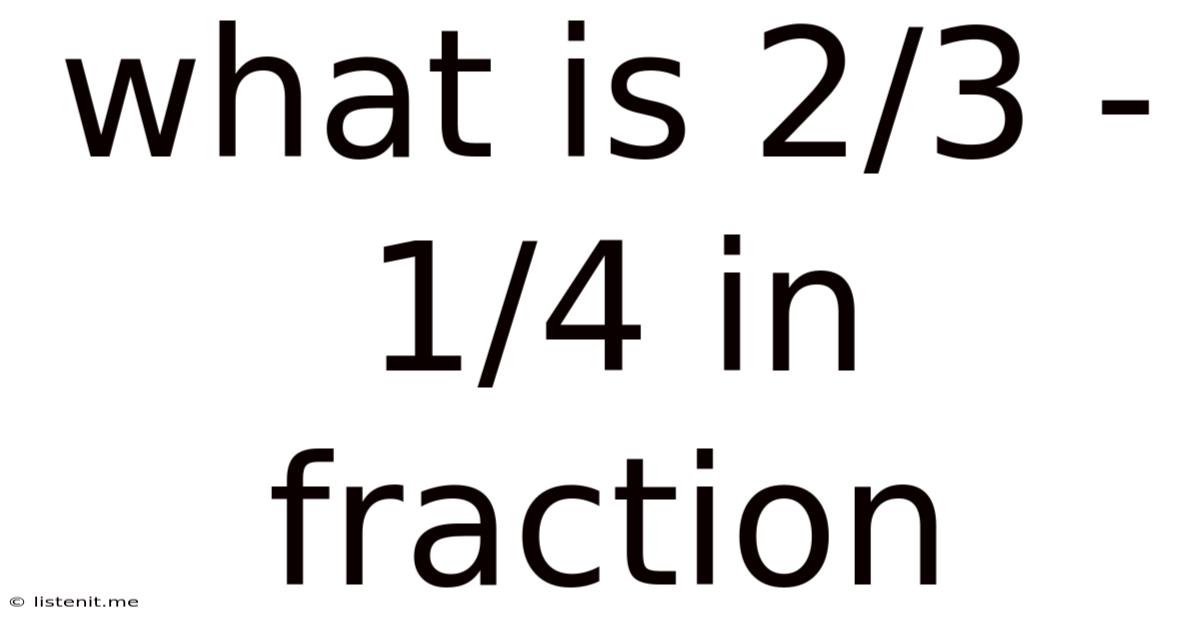
Table of Contents
What is 2/3 - 1/4 in Fraction? A Comprehensive Guide to Subtraction of Fractions
Subtracting fractions might seem daunting at first, especially when dealing with fractions that don't share a common denominator. However, with a structured approach and a clear understanding of the underlying principles, subtracting fractions like 2/3 - 1/4 becomes a straightforward process. This comprehensive guide will walk you through the steps, explain the concepts, and provide you with practical examples to solidify your understanding. We'll explore various methods, highlighting the most efficient techniques for solving this and similar problems.
Understanding the Basics: Fractions and Common Denominators
Before diving into the subtraction, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In our problem, 2/3 - 1/4, we have two fractions:
- 2/3: The numerator is 2, and the denominator is 3. This means we have 2 parts out of a total of 3 equal parts.
- 1/4: The numerator is 1, and the denominator is 4. This means we have 1 part out of a total of 4 equal parts.
The Crucial Role of the Common Denominator:
The core principle in adding or subtracting fractions is to have a common denominator. This means that the bottom numbers (denominators) of both fractions must be the same. You can't directly subtract 1/4 from 2/3 because they represent different sizes of parts. Imagine trying to subtract one quarter of a pizza from two-thirds of a different pizza – it doesn't make immediate sense.
We need to find a common denominator – a number that is a multiple of both 3 and 4.
Finding the Least Common Denominator (LCD)
The most efficient approach is to find the least common denominator (LCD). This is the smallest number that is a multiple of both denominators. There are several ways to find the LCD:
1. Listing Multiples:
List the multiples of each denominator until you find a common multiple:
- Multiples of 3: 3, 6, 9, 12, 15, 18...
- Multiples of 4: 4, 8, 12, 16, 20...
The smallest common multiple is 12. Therefore, the LCD of 3 and 4 is 12.
2. Prime Factorization:
This method is particularly useful for larger numbers. It involves breaking down each denominator into its prime factors:
- 3 = 3 (3 is a prime number)
- 4 = 2 x 2 (2 is a prime number)
To find the LCD, take the highest power of each prime factor present in either factorization:
- LCD = 2 x 2 x 3 = 12
Converting Fractions to the Common Denominator
Once we've found the LCD (12), we need to convert both fractions so they have this denominator. We do this by multiplying the numerator and the denominator of each fraction by the appropriate factor:
-
For 2/3: To get a denominator of 12, we need to multiply the denominator (3) by 4. To maintain the value of the fraction, we must also multiply the numerator (2) by 4:
(2/3) x (4/4) = 8/12
-
For 1/4: To get a denominator of 12, we need to multiply the denominator (4) by 3. Again, we must also multiply the numerator (1) by 3:
(1/4) x (3/3) = 3/12
Performing the Subtraction
Now that both fractions have the same denominator (12), we can subtract the numerators:
8/12 - 3/12 = (8 - 3)/12 = 5/12
Therefore, 2/3 - 1/4 = 5/12
Simplifying the Result (If Necessary)
In this case, 5/12 is already in its simplest form. A fraction is simplified when the numerator and denominator have no common factors other than 1. If the resulting fraction could be simplified, we would divide both the numerator and denominator by their greatest common divisor (GCD).
Alternative Methods and Visual Representations
While the method above is the most common and efficient, let's explore alternative approaches to enhance your understanding:
1. Visual Representation:
Imagine two circles. Divide one circle into three equal parts and shade two of them (representing 2/3). Divide the other circle into four equal parts and shade one (representing 1/4). Visually comparing the shaded areas helps illustrate the concept of finding a common unit to compare. This reinforces the need for a common denominator.
2. Using a Calculator:
While it's crucial to understand the underlying mathematical principles, calculators can be used to verify the result. Most calculators have the capability to handle fraction calculations. Inputting 2/3 - 1/4 will yield the decimal equivalent of 5/12, which can then be converted back to a fraction if necessary.
Expanding on Fraction Subtraction: More Complex Examples
Let's extend our understanding by examining more complex scenarios:
Example 1: Subtracting Fractions with Larger Numbers and Different Denominators
Let's solve 7/15 - 2/9.
-
Find the LCD: The LCD of 15 and 9 is 45 (3 x 3 x 5).
-
Convert to the LCD:
- 7/15 x (3/3) = 21/45
- 2/9 x (5/5) = 10/45
-
Subtract: 21/45 - 10/45 = 11/45
Therefore, 7/15 - 2/9 = 11/45
Example 2: Mixed Numbers
Mixed numbers consist of a whole number and a fraction (e.g., 2 1/3). To subtract mixed numbers, you can either:
- Convert to Improper Fractions: Convert each mixed number into an improper fraction (where the numerator is larger than the denominator). Then follow the steps for subtracting regular fractions.
- Subtract Whole Numbers and Fractions Separately: Subtract the whole numbers, then subtract the fractions. If the fraction part of the second mixed number is larger than the first, you might need to borrow from the whole number.
Conclusion: Mastering Fraction Subtraction
Subtracting fractions, even those with dissimilar denominators, is a fundamental skill in mathematics. By understanding the core concepts of common denominators, least common denominators, and the process of converting fractions, you can confidently tackle a wide range of fraction subtraction problems. Remember to practice regularly to solidify your understanding and improve your efficiency. The methods and examples provided in this guide will equip you with the tools to master fraction subtraction and apply it to various mathematical contexts. Whether you're working on simple problems or tackling more complex equations involving mixed numbers, the principles outlined here remain consistent. Consistent practice and a clear understanding of the steps involved are key to building confidence and proficiency in fraction subtraction.
Latest Posts
Latest Posts
-
What Is The Main Goal Of Long Term Care
Jun 05, 2025
-
What Is The Key Characteristic Of A Transformed Cell
Jun 05, 2025
-
Primary Care Versus Primary Health Care
Jun 05, 2025
-
The Evolution Of Eukaryotic Cells Most Likely Involved
Jun 05, 2025
-
P Wave Inversion In V1 And V2
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 - 1/4 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.