What Is 18 As A Fraction
listenit
Apr 02, 2025 · 6 min read
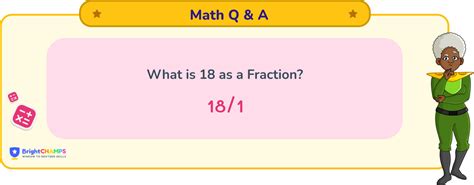
Table of Contents
What is 18 as a Fraction? A Comprehensive Guide
The seemingly simple question, "What is 18 as a fraction?" opens the door to a deeper understanding of fractions, their various representations, and their significance in mathematics. While the immediate answer might seem straightforward, exploring the nuances of representing whole numbers as fractions reveals crucial concepts applicable across various mathematical fields. This comprehensive guide will explore not only the basic conversion but also delve into the different forms a fraction representing 18 can take, its applications, and the broader implications of understanding fractional representations.
Understanding Fractions: A Quick Refresher
Before we dive into expressing 18 as a fraction, let's revisit the fundamental concepts of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator (representing 3 parts), and 4 is the denominator (representing a whole divided into 4 equal parts).
Expressing 18 as a Fraction: The Basics
The simplest way to express the whole number 18 as a fraction is to place it over 1. This is because any number divided by 1 equals itself. Therefore, 18/1 is the most basic fractional representation of 18. This is equivalent to saying you have 18 parts out of a total of 1 part, which effectively means you have the whole of 18.
Equivalent Fractions: Infinite Possibilities
It's crucial to understand the concept of equivalent fractions. Equivalent fractions represent the same value but have different numerators and denominators. For instance, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions representing the same value – one-half. This concept applies to 18 as well. We can create countless equivalent fractions by multiplying both the numerator and denominator of 18/1 by the same number.
Here are a few examples of equivalent fractions for 18:
- 36/2: (18 x 2) / (1 x 2)
- 54/3: (18 x 3) / (1 x 3)
- 72/4: (18 x 4) / (1 x 4)
- 90/5: (18 x 5) / (1 x 5)
- 180/10: (18 x 10) / (1 x 10)
and so on... The possibilities are infinite. Each of these fractions, while appearing different, all represent the same value: 18.
Simplifying Fractions: Finding the Lowest Terms
While we can create infinitely many equivalent fractions for 18, it's often beneficial to express a fraction in its simplest form, also known as the lowest terms. This means reducing the fraction to its smallest possible numerator and denominator while maintaining its value. In the case of 18/1, it's already in its simplest form because 18 and 1 share no common factors other than 1.
However, if we start with a more complex equivalent fraction like 36/2, we can simplify it by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 36 and 2 is 2. Dividing both the numerator and denominator by the GCD gives us:
36/2 = (36 ÷ 2) / (2 ÷ 2) = 18/1
This demonstrates that even though we started with a different equivalent fraction, simplifying it leads us back to the simplest form, 18/1.
Applications of Representing 18 as a Fraction
Understanding the fractional representation of whole numbers like 18 extends beyond basic arithmetic. Its applications span various fields:
1. Proportions and Ratios:
Fractions are essential for representing proportions and ratios. For example, if you have a recipe that calls for 18 ounces of flour and you want to scale it down to half the size, you would use a fraction (1/2) to calculate the amount of flour needed (18 x 1/2 = 9 ounces).
2. Geometry and Measurement:
In geometry, fractions are crucial for representing parts of shapes or measurements. If you have a 18-inch long piece of wood and need to cut it into equal pieces, fractions can help determine the length of each piece.
3. Probability and Statistics:
Fractions are used extensively in probability and statistics to represent the likelihood of events. For instance, if you have a bag containing 18 red marbles and 2 blue marbles, the probability of picking a red marble is expressed as 18/20, which simplifies to 9/10.
4. Algebra and Advanced Mathematics:
The concept of expressing whole numbers as fractions is a fundamental building block in algebra and more advanced mathematical concepts. It lays the groundwork for understanding rational numbers, algebraic manipulations, and solving complex equations.
Beyond the Basics: Exploring Mixed Numbers and Improper Fractions
While 18/1 is the most straightforward representation, we can also express 18 using mixed numbers and improper fractions.
Improper Fractions: An improper fraction is a fraction where the numerator is greater than or equal to the denominator. We can create improper fractions equivalent to 18 by choosing a denominator and calculating the corresponding numerator. For example:
- 36/2 (as discussed before)
- 54/3
- 72/4
- and so on...
Mixed Numbers: A mixed number combines a whole number and a proper fraction (where the numerator is less than the denominator). While 18 itself is a whole number, if we were dealing with a slightly different scenario, understanding mixed numbers becomes crucial. For instance, if we had 18 and a fraction of something, we could represent it as a mixed number. For example, 18 ¾ is a mixed number. To convert this into an improper fraction, you would multiply the whole number by the denominator, add the numerator, and then keep the same denominator: (18 x 4) + 3 / 4 = 75/4. This concept is particularly useful when working with measurements or quantities that include both whole units and parts of units.
Conclusion: The Significance of Fractional Representation
The seemingly simple act of representing 18 as a fraction opens up a world of mathematical possibilities. Understanding equivalent fractions, simplifying fractions, and appreciating the different ways a whole number can be expressed fractionally are crucial skills that extend far beyond elementary arithmetic. Mastering these concepts lays a solid foundation for success in higher-level mathematics, while also providing valuable tools applicable to numerous real-world scenarios across various fields. From recipes to probability calculations, the ability to comfortably work with fractions is an invaluable asset. This comprehensive guide has explored the core concepts, providing a thorough understanding of what it means to represent 18 as a fraction and highlighting the broader implications of mastering this fundamental mathematical skill.
Latest Posts
Latest Posts
-
How Many Square Yards In A Mile
Apr 03, 2025
-
What Is The Square Root Of 104
Apr 03, 2025
-
How Much Is 1500 Ml In Liters
Apr 03, 2025
-
What Is The Decimal Of 60
Apr 03, 2025
-
Solving Linear Systems By Substitution Answer Key
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is 18 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
