What Is 16 To The Power Of 2
listenit
May 25, 2025 · 5 min read
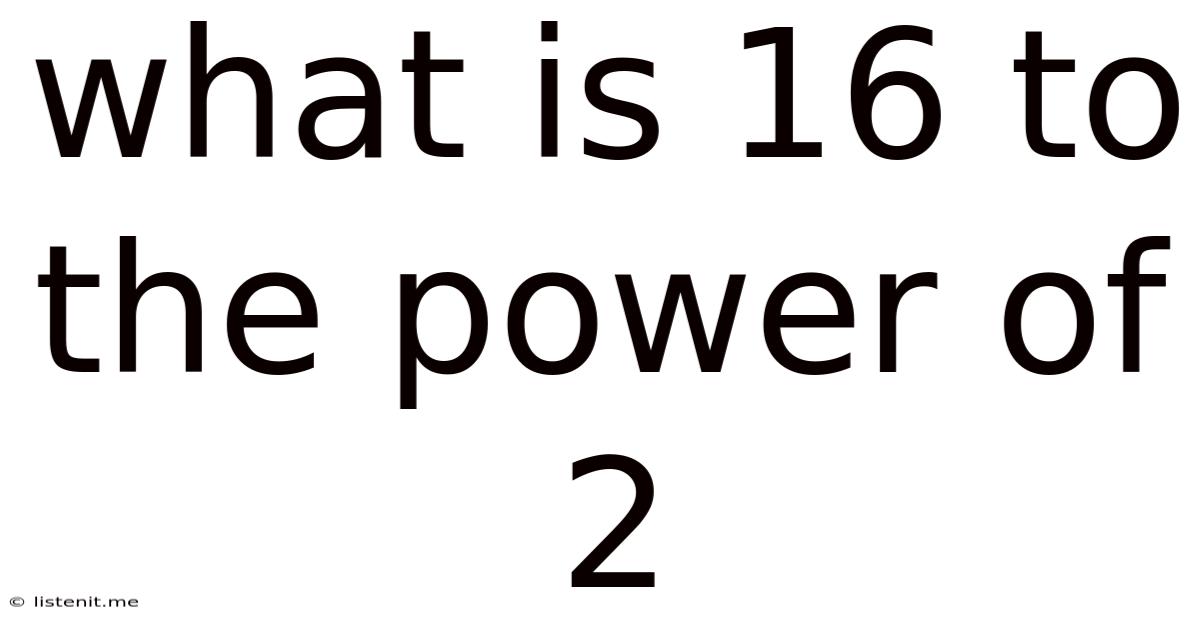
Table of Contents
What is 16 to the Power of 2? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What is 16 to the power of 2?" opens a door to a fascinating world of mathematics, specifically the realm of exponents. While the answer itself is straightforward (256), understanding the underlying concepts and the broader implications of exponentiation offers significant value, impacting numerous fields from basic arithmetic to advanced scientific calculations. This comprehensive exploration will delve into the meaning of exponents, demonstrate different methods of solving 16², explore real-world applications, and uncover the rich mathematical tapestry interwoven with this fundamental concept.
Understanding Exponents: A Foundation for Calculation
Before we tackle 16², let's establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expression b<sup>n</sup>, 'b' represents the base, and 'n' represents the exponent. This expression is read as "b raised to the power of n" or "b to the nth power."
For example:
- 2<sup>3</sup> = 2 x 2 x 2 = 8 (2 is multiplied by itself 3 times)
- 5<sup>2</sup> = 5 x 5 = 25 (5 is multiplied by itself 2 times)
- 10<sup>4</sup> = 10 x 10 x 10 x 10 = 10000 (10 is multiplied by itself 4 times)
The Significance of the Exponent "2" (Squaring)
When the exponent is 2, we're dealing with a specific operation called "squaring." Squaring a number means multiplying it by itself. Geometrically, squaring a number represents the area of a square with sides of that length. This visual representation makes understanding squaring intuitive and relatable. For instance, 5² represents the area of a square with sides of length 5 units (5 x 5 = 25 square units).
Calculating 16 to the Power of 2: Multiple Approaches
Now, let's directly address the question: What is 16²? Several methods can be employed to arrive at the correct answer:
Method 1: Direct Multiplication
The most straightforward approach is direct multiplication:
16² = 16 x 16 = 256
This method is simple and easily understood, making it ideal for beginners.
Method 2: Using the Properties of Exponents
Exponent rules offer alternative, sometimes more efficient, ways to calculate powers. For example, we can rewrite 16 as 2⁴. Therefore:
16² = (2⁴)²
Using the power of a power rule ( (a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup> ), we get:
(2⁴)² = 2<sup>(4x2)</sup> = 2<sup>8</sup>
Now, we can calculate 2<sup>8</sup>:
2<sup>8</sup> = 256
This method demonstrates the power of manipulating exponential expressions to simplify calculations.
Method 3: Utilizing a Calculator
For larger exponents or more complex calculations, a calculator is an invaluable tool. Simply input "16²" or "16^2" (depending on your calculator's syntax) to obtain the result: 256. Calculators are efficient for solving such problems quickly, particularly in real-world applications where speed is essential.
Real-World Applications of Exponents and Squaring
The concept of exponents, particularly squaring, isn't confined to the realm of theoretical mathematics. It permeates various aspects of our lives:
1. Geometry and Area Calculations:
As previously mentioned, squaring a number directly relates to calculating the area of a square. This extends to other geometric calculations. For example, finding the area of a circle involves squaring the radius (A = πr²). Similar applications arise in calculating the surface area and volume of various three-dimensional shapes.
2. Physics and Engineering:
Exponents are crucial in physics and engineering. For instance, calculating kinetic energy involves squaring the velocity (KE = ½mv²). Newton's Law of Universal Gravitation also utilizes exponents, showcasing the relationship between gravitational force, mass, and distance. Understanding exponents is fundamental for interpreting and solving many physics and engineering problems.
3. Computer Science and Data Storage:
In computer science, exponents are fundamental to understanding data storage and processing. Data is often measured in powers of 2 (kilobytes, megabytes, gigabytes, etc.), making an understanding of exponents essential for programmers and data scientists. The binary number system, the foundation of computing, relies heavily on powers of 2.
4. Finance and Compound Interest:
The power of compounding in finance is a direct application of exponents. Compound interest calculations involve raising the principal amount to a power determined by the number of compounding periods. This showcases how small, consistent investments can yield significant returns over time. Understanding exponential growth is crucial for financial planning and investment strategies.
5. Statistics and Probability:
In statistics and probability, exponents are encountered in various distributions, such as the normal distribution. Understanding the properties of exponential functions is critical for interpreting statistical data and making informed decisions based on probability.
Beyond 16²: Exploring Higher Powers and Exponential Growth
While we've focused on 16², the principles extend to higher powers and more complex exponential expressions. Understanding exponential growth is critical in numerous contexts:
- Population Growth: Modeling population growth often uses exponential functions to reflect the rapid increase in population over time.
- Spread of Diseases: The spread of contagious diseases can also be modeled using exponential functions, highlighting the importance of proactive measures to control outbreaks.
- Technological Advancement: Technological advancements, particularly in computing power, often exhibit exponential growth, leading to rapid changes in society and industry.
Conclusion: The Enduring Significance of Exponents
The seemingly simple calculation of 16² unlocks a deeper understanding of exponents and their far-reaching applications. From basic geometry to advanced scientific calculations and financial modeling, the concept of exponentiation forms a cornerstone of mathematical understanding. By mastering the principles of exponents and their various properties, we equip ourselves with valuable tools for solving diverse problems and interpreting complex phenomena in the world around us. The answer to "What is 16 to the power of 2?" is 256, but the journey to understanding the underlying principles is far more significant and rewarding. This exploration highlights the beauty and power of mathematics and its essential role in comprehending the complexities of our world.
Latest Posts
Latest Posts
-
10 Out Of 23 As A Percentage
May 25, 2025
-
What Is The Gcf Of 18 And 35
May 25, 2025
-
What Is 72 Hours From Monday At 6pm
May 25, 2025
-
How Old Are You If Your Born In 1982
May 25, 2025
-
25 5 Is What Percent Of 85
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 16 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.