What Is 15 Percent Of 10
listenit
May 25, 2025 · 5 min read
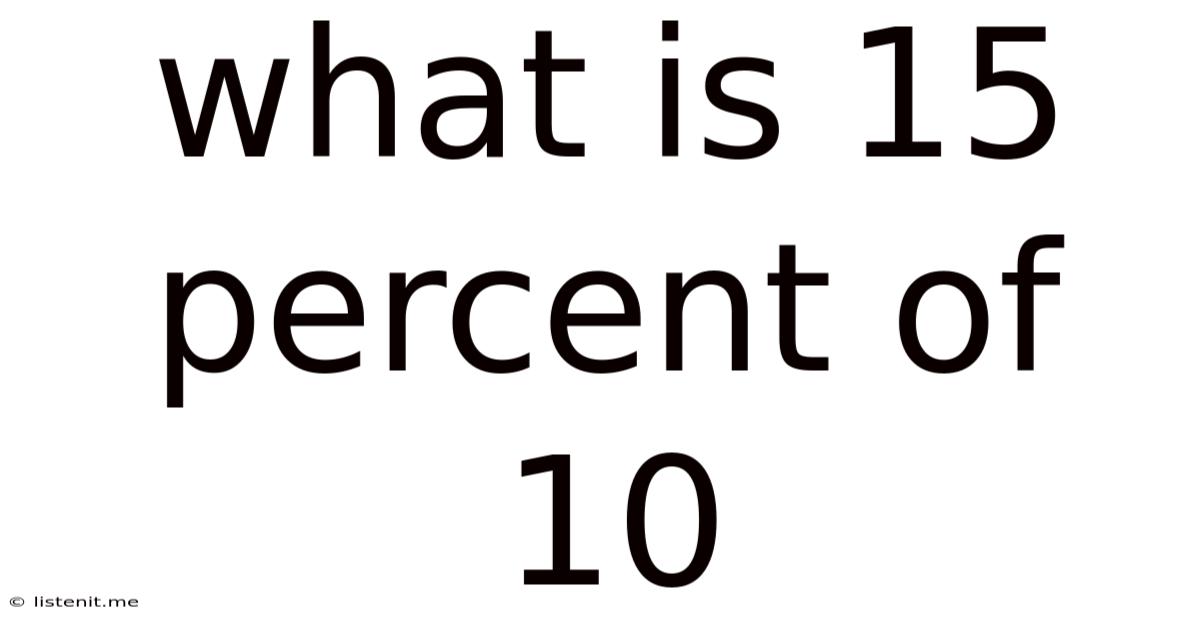
Table of Contents
What is 15 Percent of 10? A Deep Dive into Percentages and Their Applications
The seemingly simple question, "What is 15 percent of 10?" opens a door to a vast world of mathematical concepts and practical applications. While the answer itself is straightforward – 1.5 – understanding the underlying principles and exploring the broader context of percentages is crucial for navigating various aspects of life, from everyday finances to complex scientific calculations. This article will delve deep into the meaning of percentages, explore different methods to calculate 15% of 10, and showcase the diverse applications of percentage calculations in real-world scenarios.
Understanding Percentages: A Foundation
Before tackling the specific calculation, let's establish a firm understanding of what percentages represent. A percentage is simply a fraction or a ratio expressed as a part of 100. The symbol "%" signifies "per hundred." Therefore, 15% can be interpreted as 15 out of 100, or 15/100, or 0.15 as a decimal. This understanding forms the basis for all percentage calculations.
Key Concepts:
- Percentage: A ratio or fraction expressed as a part of 100.
- Decimal: The equivalent representation of a percentage as a number between 0 and 1. (e.g., 15% = 0.15)
- Fraction: The representation of a percentage as a fraction with a denominator of 100. (e.g., 15% = 15/100)
Calculating 15% of 10: Three Methods
There are several ways to calculate 15% of 10, each offering a unique perspective and reinforcing the underlying mathematical principles.
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the number.
- Convert the percentage to a decimal: 15% = 0.15
- Multiply the decimal by the number: 0.15 * 10 = 1.5
Therefore, 15% of 10 is 1.5.
Method 2: Using the Fraction Equivalent
This method utilizes the fractional representation of the percentage.
- Convert the percentage to a fraction: 15% = 15/100
- Multiply the fraction by the number: (15/100) * 10 = 150/100
- Simplify the fraction: 150/100 = 3/2 = 1.5
Again, 15% of 10 is 1.5. This method highlights the fundamental relationship between percentages, fractions, and decimals.
Method 3: Using Proportions
This method leverages the concept of proportions to solve the problem. We set up a proportion where we relate the percentage to the total and the unknown value (x) to the given number.
- Set up the proportion: 15/100 = x/10
- Cross-multiply: 15 * 10 = 100 * x
- Solve for x: 150 = 100x => x = 150/100 = 1.5
Once more, the answer is 1.5. This method is particularly useful when dealing with more complex percentage problems.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a fundamental skill with far-reaching applications across various fields:
Finance:
- Calculating discounts: Retail stores frequently offer discounts (e.g., 15% off). Understanding percentage calculations allows consumers to quickly determine the final price after the discount is applied.
- Calculating interest: Interest on loans, savings accounts, and investments is typically expressed as a percentage. Calculating interest earned or owed requires proficiency in percentage calculations.
- Analyzing financial statements: Financial statements, such as income statements and balance sheets, are replete with percentages. Understanding these percentages is crucial for financial analysis and decision-making. For example, profit margins, return on investment (ROI), and debt-to-equity ratios are all expressed as percentages.
- Tax calculations: Sales tax, income tax, and other taxes are often calculated as a percentage of the taxable amount.
Science and Engineering:
- Data analysis: Scientists and engineers frequently use percentages to represent data, such as experimental error, statistical significance, and composition of materials.
- Scaling and proportions: Percentage calculations are essential for scaling designs, adjusting formulas, and conducting experiments with varying quantities.
Everyday Life:
- Tip calculations: Calculating tips in restaurants often involves determining a percentage of the bill.
- Grading systems: Many educational institutions use percentages to represent grades and scores.
- Understanding statistics: News reports, polls, and surveys often present data in percentages. Understanding percentages is crucial for interpreting this information correctly.
Advanced Percentage Calculations and Concepts
Beyond the simple calculation of 15% of 10, there are more complex percentage problems that require a deeper understanding of mathematical principles. These include:
- Calculating the percentage increase or decrease: This involves determining the percentage change between two values.
- Calculating the original value after a percentage change: This is the reverse of calculating a percentage increase or decrease.
- Compound interest calculations: Compound interest involves calculating interest on the principal amount plus accumulated interest.
- Percentage points: It's important to differentiate between percentage points and percentage change. A change from 10% to 15% is a 5 percentage point increase, but a 50% increase in the percentage itself.
Mastering Percentages: A Continuous Process
Mastering percentage calculations is a journey, not a destination. Consistent practice and a deep understanding of the underlying principles are key to developing proficiency. Start with simple problems, like calculating 15% of 10, and gradually progress to more challenging problems. With dedicated effort, you can develop a strong command of percentage calculations and unlock their immense value in various aspects of your life. The seemingly simple calculation of 15% of 10 serves as a stepping stone to a broader comprehension of percentages and their significance in our numerical world. Embrace the learning process, and you'll find that the ability to work with percentages becomes an invaluable asset. Remember to practice regularly, explore different methods, and apply your knowledge to real-world problems. This will solidify your understanding and prepare you to tackle more complex percentage calculations with confidence and ease.
Latest Posts
Latest Posts
-
75 Is What Percent Of 100
May 26, 2025
-
What Is 20 Of 40 Dollars
May 26, 2025
-
What Is The Greatest Common Factor Of 24 And 84
May 26, 2025
-
How Many 2 5 Are In 1 1 2
May 26, 2025
-
How Many Days Since Oct 18
May 26, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.