What Is 14 18 As A Percent
listenit
May 25, 2025 · 4 min read
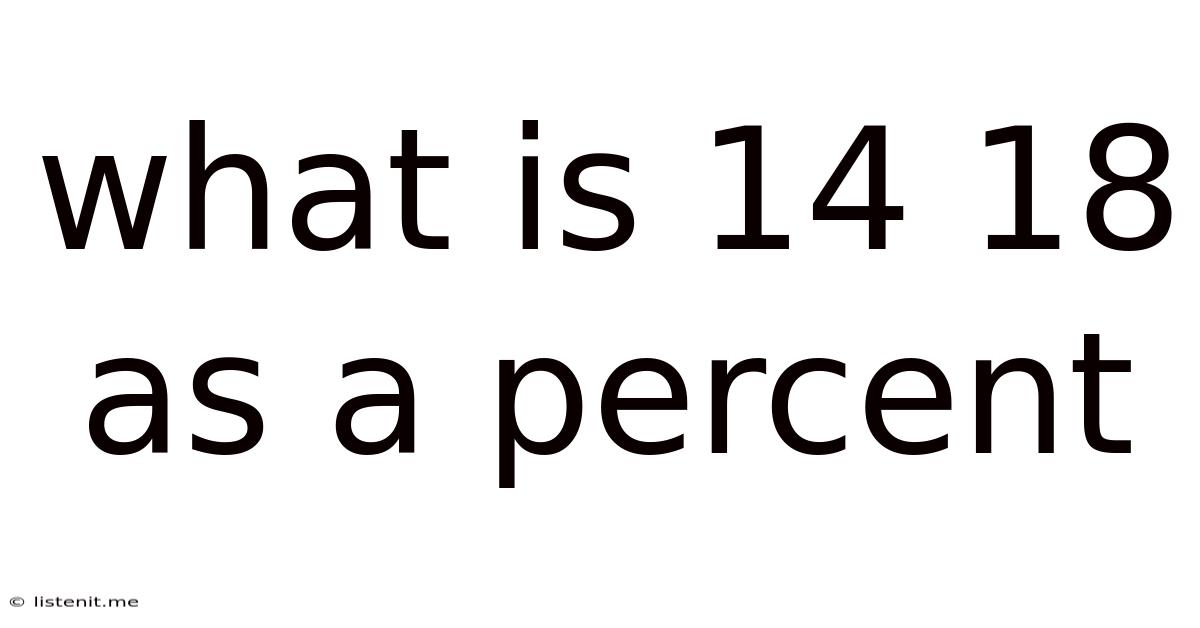
Table of Contents
What is 14/18 as a Percent? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill with broad applications in everyday life, from calculating discounts and taxes to understanding statistics and financial reports. This comprehensive guide will delve into the process of converting fractions to percentages, focusing specifically on how to express 14/18 as a percentage, and expanding on related concepts to solidify your understanding.
Understanding Fractions and Percentages
Before we dive into the calculation, let's establish a firm grasp on the core concepts. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 14/18, 14 is the numerator and 18 is the denominator. This fraction signifies 14 parts out of a total of 18 parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion relative to 100, providing a standardized way to compare different fractions. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2.
Calculating 14/18 as a Percentage: Step-by-Step Guide
To convert the fraction 14/18 into a percentage, we follow these simple steps:
Step 1: Divide the Numerator by the Denominator
The first step involves dividing the numerator (14) by the denominator (18):
14 ÷ 18 ≈ 0.7778
Step 2: Multiply the Result by 100
The result from Step 1 is a decimal. To convert this decimal to a percentage, multiply it by 100:
0.7778 x 100 = 77.78
Step 3: Add the Percentage Symbol
Finally, add the percentage symbol (%) to indicate that the result is a percentage:
77.78%
Therefore, 14/18 is approximately 77.78%.
Simplifying Fractions Before Conversion
While the above method is perfectly valid, simplifying the fraction before conversion can make the calculation easier and provide a more concise result. We can simplify 14/18 by finding the greatest common divisor (GCD) of 14 and 18, which is 2. Dividing both the numerator and denominator by 2, we get:
14 ÷ 2 = 7 18 ÷ 2 = 9
The simplified fraction is 7/9. Now, let's convert 7/9 to a percentage using the same steps as before:
7 ÷ 9 ≈ 0.7778 0.7778 x 100 = 77.78%
As you can see, we arrive at the same result, demonstrating that simplifying the fraction beforehand doesn't alter the final percentage.
Understanding the Concept of Approximation
It's important to note that the percentage we obtained (77.78%) is an approximation. The decimal 0.7778 is a recurring decimal, meaning the '7' and '8' digits repeat infinitely. We've rounded the decimal to four decimal places for practicality. Depending on the context, you might need to round to a different number of decimal places or use a more precise representation.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios. Here are a few examples:
-
Calculating Discounts: If a store offers a 20% discount on an item, you can easily calculate the discount amount and the final price using percentage calculations.
-
Determining Tax Amounts: Sales tax, income tax, and other taxes are often expressed as percentages. Understanding percentages allows you to calculate the exact tax amount.
-
Analyzing Financial Statements: Financial reports frequently use percentages to represent profit margins, growth rates, and other key financial metrics.
-
Understanding Statistics: Percentages are extensively used in statistics to represent proportions, probabilities, and other statistical measures.
-
Grading Systems: Many educational systems utilize percentages to represent grades, enabling a standardized comparison of student performance.
Advanced Percentage Calculations: Beyond the Basics
While converting a simple fraction like 14/18 to a percentage is straightforward, there are more complex scenarios you might encounter.
-
Calculating Percentage Increase or Decrease: This involves finding the percentage change between two values. For example, if a quantity increases from 100 to 120, the percentage increase is calculated as [(120-100)/100] x 100 = 20%.
-
Finding a Percentage of a Number: This involves calculating a specific percentage of a given value. For example, 25% of 200 is (25/100) x 200 = 50.
-
Working with Percentages and Fractions Simultaneously: Problems might require you to work with both fractions and percentages, requiring you to convert between these forms seamlessly.
Conclusion: Mastering Percentage Calculations
This comprehensive guide has detailed the process of calculating 14/18 as a percentage, explaining the underlying concepts and demonstrating the steps involved. Understanding percentages is a vital skill that finds application in numerous contexts. By mastering these techniques, you'll be better equipped to handle various numerical problems and interpret data effectively in various aspects of your life and career. Remember to practice regularly and explore more advanced percentage calculations to solidify your understanding and broaden your skills.
Latest Posts
Latest Posts
-
How Many Calories In Ww Points
May 25, 2025
-
What Is The Gcf Of 25 And 45
May 25, 2025
-
How To Find The Cubic Yards Of Concrete
May 25, 2025
-
What Is The Highest Common Factor Of 32 And 56
May 25, 2025
-
3 Is What Percent Of 19
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 14 18 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.