What Is 12 To The Power Of 3
listenit
May 24, 2025 · 5 min read
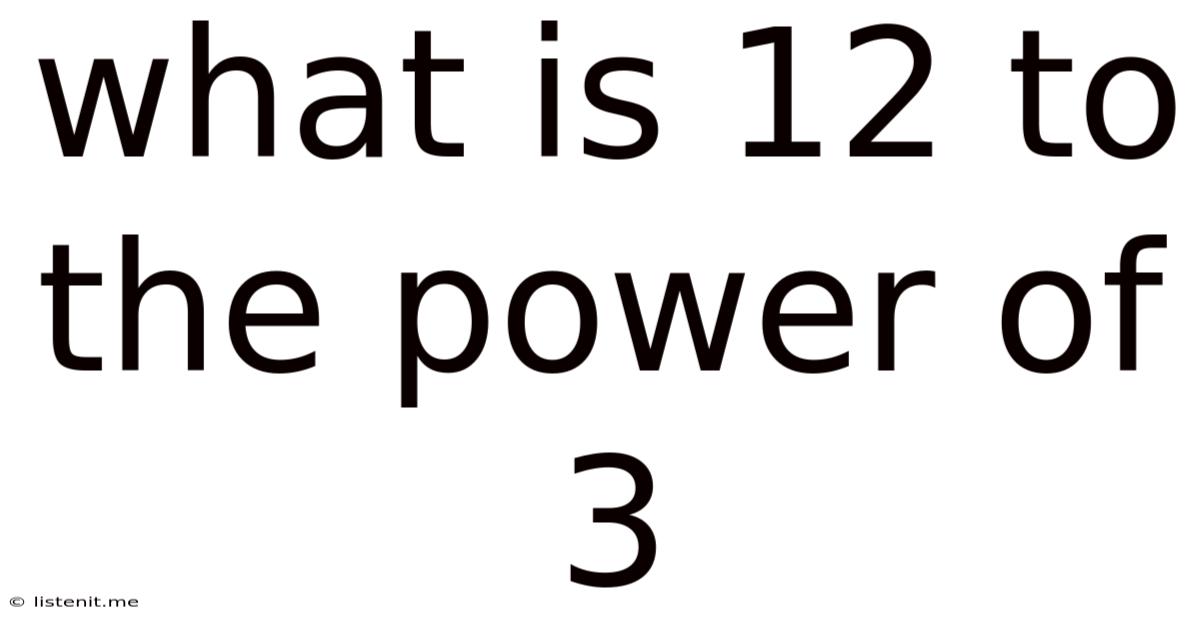
Table of Contents
What is 12 to the Power of 3? A Deep Dive into Exponentiation
The seemingly simple question, "What is 12 to the power of 3?" opens a door to a fascinating world of mathematics, specifically exponentiation. While the answer itself is easily calculated, understanding the underlying concepts and applications provides a richer appreciation of this fundamental mathematical operation. This article will not only answer the question directly but also explore the broader implications of exponentiation, its uses in various fields, and related mathematical ideas.
Understanding Exponentiation: The Basics
Exponentiation, at its core, is repeated multiplication. It's represented as a base number raised to an exponent (or power). The expression 12³ signifies that the base number, 12, is multiplied by itself three times (the exponent). Therefore, 12³ = 12 × 12 × 12.
This seemingly simple concept forms the foundation for numerous advanced mathematical concepts and has far-reaching applications across various disciplines. Let's break down the components:
- Base: This is the number being multiplied repeatedly. In our case, the base is 12.
- Exponent: This is the number indicating how many times the base is multiplied by itself. In 12³, the exponent is 3.
- Result (Power): This is the outcome of the repeated multiplication. It's the answer to the exponentiation problem.
Calculating 12 to the Power of 3
Now, let's get to the core of our question: What is 12³?
12 × 12 = 144 144 × 12 = 1728
Therefore, 12 to the power of 3 is 1728. This is a relatively straightforward calculation, especially with the assistance of a calculator. However, understanding the process behind this calculation is key to grasping the concept of exponentiation.
Beyond the Calculation: Applications of Exponentiation
The application of exponentiation extends far beyond simple arithmetic exercises. Its power lies in its ability to model various real-world phenomena and solve complex problems across multiple fields:
1. Finance and Investment: Compound Interest
Compound interest is a prime example of exponentiation in action. When interest is compounded, it's calculated not only on the principal amount but also on the accumulated interest from previous periods. This leads to exponential growth, where the returns increase dramatically over time. The formula for compound interest involves exponentiation:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
This formula showcases how even small differences in interest rates or compounding periods can lead to significantly different outcomes over time due to the exponential nature of the calculation.
2. Science and Engineering: Exponential Growth and Decay
Exponentiation is crucial in modeling various natural phenomena exhibiting exponential growth or decay. Examples include:
- Population Growth: The growth of a population often follows an exponential pattern, especially under ideal conditions with unlimited resources.
- Radioactive Decay: The decay of radioactive substances follows an exponential decay model, where the amount of radioactive material decreases exponentially over time.
- Spread of Diseases: Under certain conditions, the spread of infectious diseases can be modeled using exponential functions.
3. Computer Science: Big O Notation
In computer science, Big O notation uses exponential functions to describe the time or space complexity of algorithms. This helps programmers understand how the performance of an algorithm scales with the size of the input data. An algorithm with exponential time complexity becomes computationally infeasible for large inputs because the computation time grows exponentially with the input size.
4. Physics: Exponential Attenuation
Exponential functions play a role in describing the attenuation of signals or radiation as they travel through a medium. For example, the intensity of light decreases exponentially as it travels through a scattering medium. Similarly, the intensity of sound waves diminishes exponentially with distance from the source.
5. Chemistry: Reaction Rates
In chemical kinetics, the rate of some chemical reactions can be described by exponential functions. The concentration of reactants may decrease or the concentration of products increase exponentially over time.
Expanding on Exponentiation: Related Concepts
Understanding 12³ opens the door to understanding more complex mathematical concepts:
1. Negative Exponents
A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example, 12⁻³ = 1/(12³) = 1/1728.
2. Fractional Exponents
Fractional exponents represent roots. For example, 12^(1/2) is the square root of 12, and 12^(1/3) is the cube root of 12.
3. Zero Exponent
Any number (except zero) raised to the power of zero equals 1. For example, 12⁰ = 1.
4. Complex Exponents
Exponentiation can also be extended to complex numbers, involving imaginary units.
Practical Applications and Real-world Examples
Let's explore some tangible real-world examples that illustrate the practical uses of exponentiation:
-
Calculating the volume of a cube: If a cube has sides of 12cm, its volume is 12cm x 12cm x 12cm = 1728 cubic centimeters. This is a direct application of 12³.
-
Modeling bacterial growth: If a bacterial colony doubles in size every hour, and starts with 12 bacteria, after 3 hours there will be 12 x 2 x 2 x 2 = 96 bacteria. This illustrates exponential growth.
-
Determining the value of an investment: If you invest $12,000 at an annual interest rate of 5% compounded annually for 3 years, the future value can be calculated using the compound interest formula (mentioned earlier), demonstrating the power of exponential growth in finance.
-
Understanding radioactive decay: If a radioactive substance has a half-life of one year, and you start with 1728 grams, after three years there will be significantly less (calculated using an exponential decay formula).
Conclusion: The Significance of 12 to the Power of 3
While the answer to "What is 12 to the power of 3?" is simply 1728, the journey to finding that answer and exploring the broader context of exponentiation reveals its fundamental importance in mathematics and its wide-ranging applications in various fields. From financial modeling to scientific simulations, understanding exponentiation provides the tools to analyze, predict, and solve complex problems in our world. Its seemingly simple nature belies its profound impact on our understanding of the world around us. The seemingly basic calculation of 12³ serves as a gateway to a deeper understanding of the power and versatility of exponential functions.
Latest Posts
Latest Posts
-
How Many Btu To Heat 900 Sq Ft
May 24, 2025
-
Where Is The Calculator On The Ww App
May 24, 2025
-
What Is 30 Percent Of 125
May 24, 2025
-
Greatest Common Factor Of 24 And 84
May 24, 2025
-
20 Divided By 3 In Fraction
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 12 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.