What Is 12 Divided By 3 4
listenit
May 23, 2025 · 4 min read
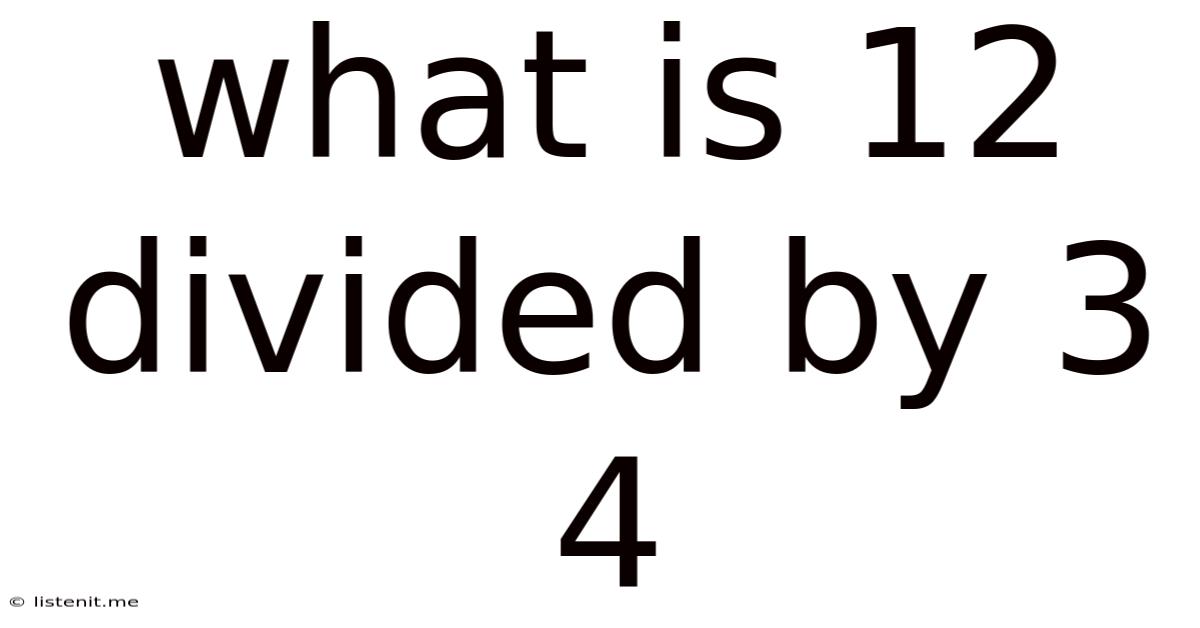
Table of Contents
What is 12 Divided by 3/4? Understanding Fraction Division
The question, "What is 12 divided by 3/4?" might seem simple at first glance, but it touches upon a crucial concept in mathematics: fraction division. Many people struggle with fractions, and understanding how to divide by them is key to mastering arithmetic and algebra. This article will thoroughly explain the process, providing multiple approaches and exploring the underlying logic to help you confidently tackle similar problems.
Understanding the Problem: 12 ÷ ¾
Before we delve into the solution, let's break down the problem: 12 ÷ ¾. This means we want to determine how many times the fraction ¾ fits into the whole number 12. Think of it like this: if you have 12 pizzas, and each serving is ¾ of a pizza, how many servings can you make?
Method 1: The Reciprocal Method (The Most Common Approach)
This is the standard method taught in schools. The core principle is to convert the division problem into a multiplication problem by using the reciprocal of the fraction.
- What is a reciprocal? The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of ¾ is ⁴⁄₃.
Here's how to apply this method to solve 12 ÷ ¾:
- Rewrite the problem: 12 ÷ ¾
- Replace division with multiplication: 12 x ⁴⁄₃
- Simplify: You can simplify before multiplying. 12 can be divided by 3, resulting in 4. So the problem becomes: 4 x ⁴⁄₁ = 16
Therefore, 12 divided by ¾ is 16.
Method 2: The Common Denominator Method
This method is less commonly used but provides a deeper understanding of the underlying principles. It involves converting the whole number into a fraction with the same denominator as the divisor.
- Convert 12 to a fraction: 12 can be written as ¹²⁄₁.
- Find a common denominator: The common denominator for ¹²⁄₁ and ¾ is 4.
- Convert fractions to a common denominator: ¹²⁄₁ becomes ⁴⁸⁄₄ (multiply numerator and denominator by 4)
- Rewrite the problem: ⁴⁸⁄₄ ÷ ¾
- Divide the numerators: 48 ÷ 3 = 16
- Keep the denominator: The denominator remains the same (although it simplifies to 1).
Therefore, 12 divided by ¾ is 16.
Method 3: Visual Representation
Visualizing the problem can be helpful, especially for beginners. Imagine dividing a 12-unit long bar into segments of ¾ units each.
- Each segment represents ¾: Draw a bar and divide it into segments of ¾ units.
- Counting the segments: Count how many segments of ¾ fit into the 12-unit bar. You will find that 16 segments fit perfectly.
This visual representation confirms that 12 divided by ¾ equals 16.
Why Does the Reciprocal Method Work?
The reciprocal method might seem like a trick, but it's grounded in mathematical principles. Division is the inverse operation of multiplication. When we divide by a fraction, we're essentially asking: "How many times does this fraction go into the whole number?" Using the reciprocal allows us to reformulate this question into a multiplication problem that's easier to solve.
Applying This Knowledge to Similar Problems
The methods described above can be applied to various division problems involving fractions. Here are a few examples:
- 20 ÷ ⅔: Using the reciprocal method: 20 x 3/2 = 30.
- 15 ÷ ⁵⁄₆: Using the reciprocal method: 15 x ⁶⁄₅ = 18.
- 8 ÷ ¼: Using the reciprocal method: 8 x ⁴⁄₁ = 32.
Remember to always follow the steps outlined above, and you'll be able to confidently solve any fraction division problem.
Common Mistakes to Avoid
When dividing by fractions, several common mistakes can lead to incorrect answers:
- Forgetting to use the reciprocal: Simply multiplying the whole number by the fraction without inverting it is a frequent error. Always remember to use the reciprocal of the divisor (the number you are dividing by).
- Incorrect simplification: Failing to simplify the numbers before multiplication can make the calculation more complex and increase the chance of mistakes. Always simplify whenever possible.
- Misunderstanding the concept of reciprocals: Ensuring a solid understanding of what reciprocals are is crucial. If you're unsure, review the definition and examples until you're comfortable.
Expanding on Fraction Division: Real-World Applications
Understanding fraction division is not just an academic exercise; it has many practical applications in everyday life:
- Cooking: Many recipes involve fractional measurements. If a recipe calls for ⅓ cup of flour per serving and you want to make 6 servings, you would need to calculate 6 ÷ ⅓ = 18 cups of flour.
- Sewing: Cutting fabric for projects frequently involves fractions of inches or centimeters. Dividing lengths of fabric based on fractional pattern pieces requires a solid understanding of fraction division.
- Construction: Calculations in construction often involve fractions of feet or meters. Determining how many pieces of lumber are needed, based on fractional measurements, is a practical application of fraction division.
- Finance: Calculating portions of investments or determining fractional shares requires proficiency with fraction division.
Conclusion: Mastering Fraction Division
Mastering fraction division is a cornerstone of mathematical proficiency. By understanding the principles behind the reciprocal method, the common denominator method, and applying the visual representation techniques, you can build confidence and accuracy in solving these types of problems. Remember to practice regularly, watch out for common errors, and appreciate the real-world relevance of this fundamental mathematical skill. The ability to confidently divide by fractions is a valuable asset applicable to numerous situations, from cooking and sewing to more complex financial calculations. It's a skill worth mastering.
Latest Posts
Latest Posts
-
How To Figure Out Triangle Side Lengths
May 23, 2025
-
Greatest Common Factor Of 30 And 80
May 23, 2025
-
3 Divided By 7 In Fraction Form
May 23, 2025
-
What Percent Of 50 Is 45
May 23, 2025
-
30 Days From November 28 2024
May 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 12 Divided By 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.