What Is 10 Divided By 1/2
listenit
May 24, 2025 · 4 min read
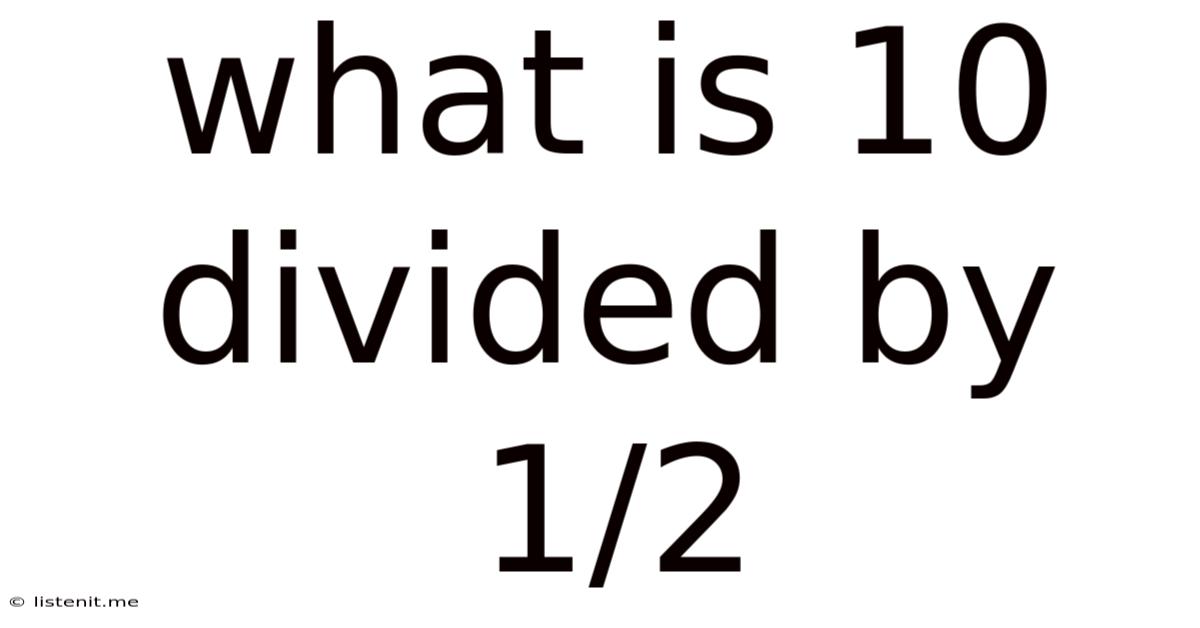
Table of Contents
What is 10 Divided by 1/2? Unpacking the Math and its Implications
The seemingly simple question, "What is 10 divided by 1/2?", often trips up even those comfortable with basic arithmetic. The answer, surprisingly, isn't 5, but rather 20. Understanding why requires a deeper dive into the principles of division with fractions. This article will not only provide the solution but also explore the underlying mathematical concepts, address common misconceptions, and even delve into real-world applications where this type of calculation is crucial.
Understanding Division: The Core Concept
Before tackling the specific problem, let's solidify our understanding of division itself. Division essentially asks, "How many times does one number fit into another?" For example, 10 ÷ 2 asks, "How many times does 2 fit into 10?" The answer, of course, is 5.
This intuitive understanding is crucial when dealing with fractions. Instead of thinking of dividing by a fraction, it's often more helpful to think of it as multiplying by its reciprocal. This is the key to solving our problem.
The Reciprocal: The Key to Fraction Division
The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/2 is 2/1, or simply 2. This is the crucial step in solving our equation.
The rule for dividing by a fraction is to multiply by its reciprocal. So, 10 ÷ 1/2 becomes 10 x 2.
Solving the Equation: 10 ÷ 1/2 = 20
Following the rule, we transform the division problem into a multiplication problem:
10 ÷ 1/2 = 10 x 2 = 20
Therefore, 10 divided by 1/2 equals 20.
Visualizing the Solution: A Practical Approach
While the mathematical rule provides a clear solution, visualizing the problem can reinforce understanding. Imagine you have 10 pizzas. If you divide each pizza into halves (1/2), how many half-pizzas do you have? You'll have 20 half-pizzas. This illustrates the answer concretely.
Addressing Common Misconceptions
The most common mistake is to incorrectly answer 5. This stems from a misunderstanding of division with fractions. Dividing by a number less than 1 (like 1/2) actually results in a larger answer. Think of it this way: dividing a quantity by a smaller number results in a larger quotient.
Expanding the Concept: Working with Other Fractions
Let's apply this principle to other examples:
-
25 ÷ 1/5: The reciprocal of 1/5 is 5. Therefore, 25 ÷ 1/5 = 25 x 5 = 125
-
12 ÷ 2/3: The reciprocal of 2/3 is 3/2. Therefore, 12 ÷ 2/3 = 12 x 3/2 = 18
-
5 ÷ 3/4: The reciprocal of 3/4 is 4/3. Therefore, 5 ÷ 3/4 = 5 x 4/3 = 20/3 or 6 and 2/3
These examples demonstrate the consistent application of the rule: multiply by the reciprocal.
Real-World Applications: Where This Matters
While this might seem like a purely theoretical mathematical exercise, dividing by fractions has practical applications across various fields:
-
Cooking and Baking: Recipes often require fractional measurements. If a recipe calls for 1/2 cup of sugar and you want to triple the recipe, you need to calculate 1.5 cups (3 x 1/2)
-
Construction and Engineering: Precision is paramount, and fractions are frequently used in measurements. Calculating material needs often involves dividing by fractions. For instance, if a project requires 1/4 of a specific material per unit and you need 10 units, you need to calculate the total material required (10 ÷ 1/4 = 40).
-
Finance: Calculating interest rates and proportions frequently involves working with fractions and decimals.
-
Science: Many scientific calculations involve dividing by fractions, from analyzing experimental data to scaling model simulations.
Beyond the Basics: Diving Deeper into Fraction Division
This fundamental understanding of fraction division forms the basis for more advanced mathematical concepts. It's crucial for understanding:
- Algebra: Solving algebraic equations often involves manipulating fractions.
- Calculus: Derivatives and integrals frequently involve working with fractions and their reciprocals.
- Advanced Physics and Engineering: Complex problems often require intricate calculations with fractions.
Mastering Fraction Division: Practice and Resources
The key to mastering fraction division, like any mathematical concept, is consistent practice. Start with simple problems, and gradually work your way towards more complex examples. Numerous online resources, including educational websites and videos, can provide further support and practice problems.
Conclusion: The Power of Understanding Fractions
The question "What is 10 divided by 1/2?" initially appears simple but highlights the importance of understanding the underlying principles of fraction division. By understanding the concept of reciprocals and applying the rule of multiplying by the reciprocal, we arrive at the correct answer: 20. This simple equation opens a door to a deeper understanding of mathematics and its wide-ranging applications in various aspects of life. Consistent practice and exploration of related concepts will strengthen your mathematical skills and build a solid foundation for more advanced studies. Remember the power of visualization and apply these principles to solve real-world problems.
Latest Posts
Latest Posts
-
How To Calculate Car Loan Payoff Amount
May 24, 2025
-
What Is 3 Divided By 27
May 24, 2025
-
How Fast Is 250 Kilometers Per Hour
May 24, 2025
-
4000 Btu Air Conditioner Room Size
May 24, 2025
-
23 Years Old What Year Born
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Divided By 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.