What Is 1 Divided By 1 5
listenit
May 24, 2025 · 5 min read
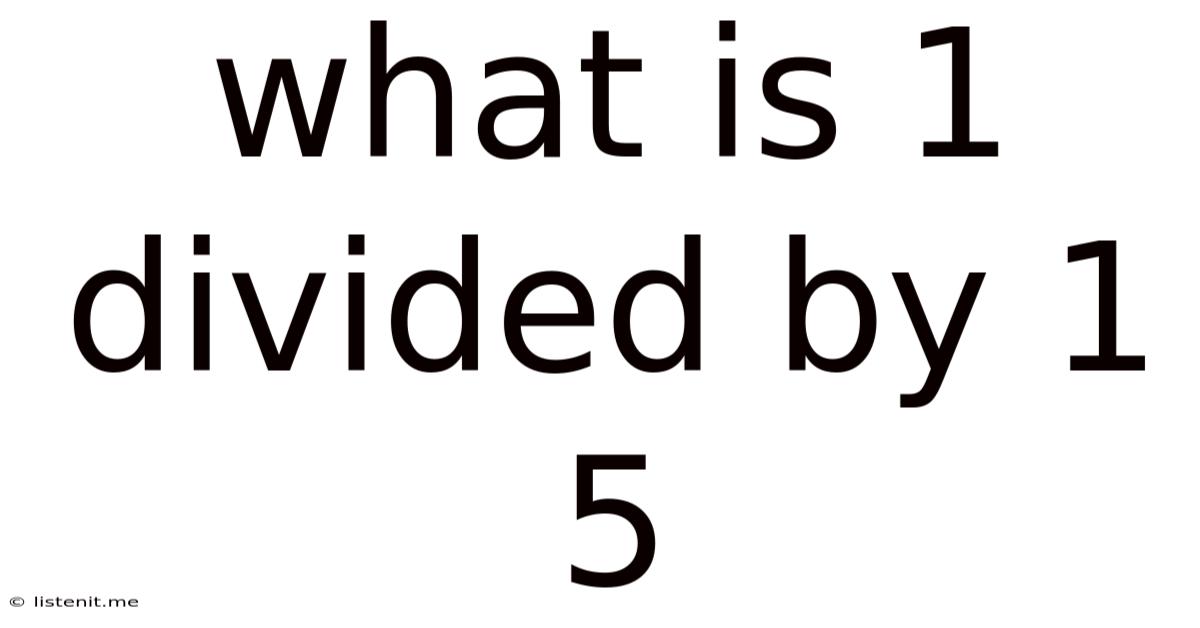
Table of Contents
What is 1 Divided by 1/5? Understanding Fractions and Division
The seemingly simple question, "What is 1 divided by 1/5?", often trips up individuals unfamiliar with fraction division. While it might appear daunting at first glance, understanding the underlying principles of fraction manipulation makes it remarkably straightforward. This article will delve into the intricacies of this calculation, explaining the process step-by-step, exploring the underlying mathematical concepts, and providing practical examples to solidify your understanding. We’ll also touch upon real-world applications to showcase the relevance of this seemingly abstract mathematical operation.
Understanding the Basics: Fractions and Division
Before tackling the specific problem, let's refresh our understanding of fractions and division. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
Division, on the other hand, is the process of splitting a quantity into equal parts. When we divide 1 by 1/5, we're essentially asking, "How many times does 1/5 fit into 1?"
The "Keep, Change, Flip" Method
The most common and efficient method for dividing fractions is the "keep, change, flip" (or "invert and multiply") method. Here's how it works:
-
Keep: Keep the first fraction (in this case, 1, which can be written as 1/1) exactly as it is.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip (or invert) the second fraction. This means swapping the numerator and the denominator. So, 1/5 becomes 5/1.
Applying this to our problem:
1 ÷ 1/5 becomes 1/1 × 5/1
Now, we simply multiply the numerators together and the denominators together:
(1 × 5) / (1 × 1) = 5/1 = 5
Therefore, 1 divided by 1/5 is 5.
Visualizing the Solution
It's often helpful to visualize mathematical concepts. Imagine you have a single pizza (representing the number 1). If you cut the pizza into five equal slices (representing 1/5), how many slices do you have? You have five slices. This visually confirms that 1 divided by 1/5 equals 5.
Real-World Applications
Understanding fraction division isn't just an academic exercise; it has practical applications in numerous real-world scenarios:
-
Cooking and Baking: Recipes often require dividing ingredients. For instance, if a recipe calls for 1/5 of a cup of sugar and you want to make five times the recipe, you would need to calculate 5 x (1/5 cup) = 1 cup of sugar.
-
Construction and Measurement: Carpenters, builders, and engineers frequently work with fractions when measuring materials and calculating dimensions. Dividing lengths or quantities often involves fractional calculations.
-
Finance and Budgeting: Dividing budgets, calculating shares, or understanding percentages all involve fraction manipulation. For example, if you have $1 and want to allocate it equally among five projects, you'd divide 1 by 1/5 to determine the amount allocated to each project.
-
Data Analysis and Statistics: Fractions and division are fundamental in statistical analysis, where data is often represented as fractions or proportions.
Exploring Related Concepts: Reciprocal and Multiplicative Inverse
The "flip" step in the "keep, change, flip" method is directly related to the concept of a reciprocal (also known as a multiplicative inverse). The reciprocal of a number is simply 1 divided by that number. For instance, the reciprocal of 5 is 1/5, and the reciprocal of 1/5 is 5. When dividing by a fraction, we are essentially multiplying by its reciprocal.
This concept is crucial for a deeper understanding of why the "keep, change, flip" method works. By flipping the second fraction and changing the division to multiplication, we are essentially using the multiplicative inverse to simplify the calculation.
Dealing with More Complex Fractions
The principles discussed above can be applied to more complex fraction division problems. Let's consider a slightly more challenging example:
What is 2/3 divided by 1/6?
-
Keep: Keep the first fraction as 2/3.
-
Change: Change the division sign to a multiplication sign.
-
Flip: Flip the second fraction, making it 6/1.
Now, multiply:
(2/3) × (6/1) = (2 × 6) / (3 × 1) = 12/3 = 4
Therefore, 2/3 divided by 1/6 is 4.
Avoiding Common Mistakes
While the "keep, change, flip" method is efficient, some common mistakes can lead to incorrect results. Here are a few to watch out for:
-
Forgetting to flip the second fraction: This is the most common error. Always remember to invert the second fraction before multiplying.
-
Incorrectly multiplying the numerators and denominators: Pay close attention to the multiplication process to avoid errors.
-
Simplifying fractions improperly: Make sure to simplify the resulting fraction to its lowest terms.
-
Misinterpreting mixed numbers: If you're working with mixed numbers (e.g., 2 1/2), convert them to improper fractions before applying the "keep, change, flip" method.
Practice Problems
To solidify your understanding, try solving these practice problems:
-
3 ÷ 1/4 = ?
-
1/2 ÷ 1/3 = ?
-
2 1/2 ÷ 1/5 = ?
-
5/8 ÷ 2/3 = ?
-
1/10 ÷ 1/100 = ?
Remember to apply the "keep, change, flip" method and simplify your answers. The answers are provided at the end of this article.
Conclusion
Understanding how to divide fractions is a crucial skill with wide-ranging applications. The "keep, change, flip" method provides a simple and effective way to solve these problems, enabling you to confidently tackle fraction division in various contexts. By mastering this concept, you’ll enhance your mathematical capabilities and better understand the world around you.
Answers to Practice Problems:
- 12
- 3/2 or 1 1/2
- 25/2 or 12 1/2
- 15/16
- 10
This comprehensive guide helps you not only solve "1 divided by 1/5" but also equips you with a thorough understanding of fraction division, enabling you to confidently tackle more complex problems. Remember to practice regularly and apply these concepts to real-world scenarios to solidify your understanding.
Latest Posts
Latest Posts
-
6 Out Of 10 Is What Percent
May 24, 2025
-
Greatest Common Factor 16 And 36
May 24, 2025
-
Least Common Multiple 3 5 7
May 24, 2025
-
What Is 2 3 Divided By 8
May 24, 2025
-
20 Out Of 21 As A Percentage
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 Divided By 1 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.