What Is 1 8 Divided By 3 4
listenit
May 24, 2025 · 5 min read
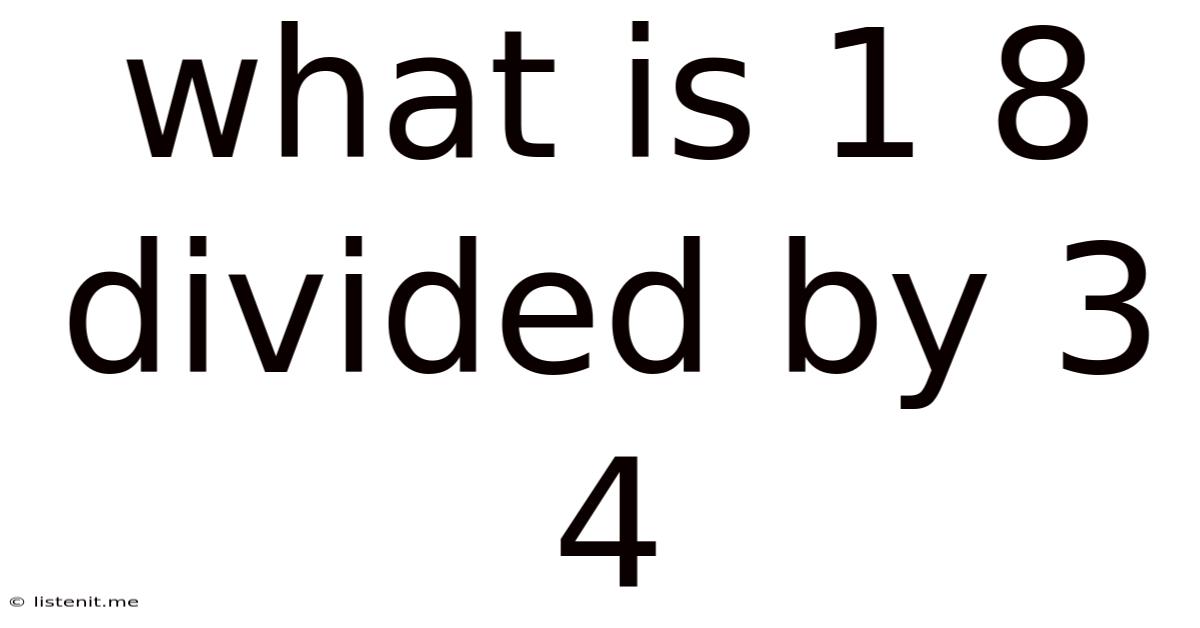
Table of Contents
What is 1 8 Divided by 3 4? A Comprehensive Guide to Fraction Division
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This article will thoroughly explain how to solve the problem "What is 1 8 divided by 3 4?" and provide a broader understanding of fraction division, equipping you with the skills to tackle similar problems with confidence.
Understanding Fractions and Mixed Numbers
Before diving into the division, let's refresh our understanding of fractions and mixed numbers. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
A mixed number combines a whole number and a fraction, for example, 1 8. This means we have one whole unit and 8 parts of another unit, where the unit is divided into some number of equal parts (the denominator of the fraction). In this case, the mixed number 1 8 should be considered as having a denominator that is understood, but not explicitly stated, so that is not necessarily the same as 1 8/1. This will become important later in the article.
Converting Mixed Numbers to Improper Fractions
To divide fractions effectively, it's often easier to work with improper fractions. An improper fraction has a numerator that is greater than or equal to its denominator. To convert a mixed number to an improper fraction, follow these steps:
- Multiply the whole number by the denominator of the fraction.
- Add the result to the numerator.
- Keep the same denominator.
Let's convert 1 8 into an improper fraction. Assuming a denominator of 1 (as in 1 8/1):
- 1 (whole number) * 1 (denominator) = 1
- 1 (result) + 8 (numerator) = 9
- The denominator remains 1.
Therefore, 1 8 as an improper fraction is 9/1.
Note: It is important to understand the context of the mixed number. If the problem was written as "1 and 8 divided by 3 and 4" then the mixed numbers should be considered as 1 8/1 and 3 4/1 respectively. This will change the final answer, and demonstrates the importance of precise problem statements.
Dividing Fractions: The Reciprocal Method
Dividing fractions involves a crucial step: finding the reciprocal of the second fraction (the divisor). The reciprocal of a fraction is simply the fraction flipped upside down; the numerator becomes the denominator, and the denominator becomes the numerator.
For example, the reciprocal of 3/4 is 4/3.
Once you have the reciprocal, the division problem transforms into a multiplication problem:
Fraction 1 ÷ Fraction 2 = Fraction 1 × Reciprocal of Fraction 2
Solving the Problem: 1 8 Divided by 3 4
Now let's apply these steps to solve "What is 1 8 divided by 3 4?". We will address the problem in two separate ways, once assuming the problem is 1 8/1 divided by 3 4/1 and then again clarifying the ambiguity.
Method 1 (Assuming 1 8/1 divided by 3 4/1):
-
Convert mixed numbers to improper fractions: As shown above, 1 8/1 becomes 9/1, and 3 4/1 becomes 7/1.
-
Find the reciprocal of the second fraction: The reciprocal of 7/1 is 1/7.
-
Multiply the fractions: 9/1 × 1/7 = 9/7
-
Simplify the result (if possible): 9/7 is an improper fraction, which can be converted to a mixed number: 1 2/7
Therefore, using this method, 1 8/1 divided by 3 4/1 equals 1 2/7.
Method 2 (Clarifying the ambiguity of the problem):
The original question, "What is 1 8 divided by 3 4?" is ambiguous. The phrasing is unclear about whether it intends to represent mixed numbers (1 8/1 and 3 4/1) or a different representation of decimal numbers.
If we consider the question as referring to the decimal numbers 1.8 and 3.4, then the solution is:
1.8 ÷ 3.4 ≈ 0.529
This answer is significantly different from the answer obtained using the mixed number interpretation in Method 1. This highlights the need for careful and clear problem definition and the avoidance of ambiguity.
This demonstrates the importance of precisely stating mathematical problems. Ambiguity can lead to multiple interpretations and different results. If the intention was to use mixed numbers, the problem statement should have been clearer.
Advanced Fraction Division Techniques
While the reciprocal method is generally the most efficient, let's explore a few alternative approaches for a more holistic understanding.
The Common Denominator Method
This method involves converting both fractions to equivalent fractions with the same denominator before dividing the numerators. While this works for simple fractions, it quickly becomes tedious for complex fractions. It's less efficient than the reciprocal method, especially when dealing with mixed numbers.
Using Decimal Conversions
Another approach is to convert both fractions into decimals before performing the division. This is straightforward but introduces the possibility of rounding errors, which might affect the accuracy of the result depending on the number of decimal places considered. This method is suitable only for certain problems, particularly when a decimal approximation is acceptable.
Practical Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it finds practical applications in numerous real-world scenarios. Consider these examples:
- Cooking and Baking: Scaling recipes up or down often requires dividing fractions.
- Sewing and Tailoring: Calculating fabric requirements involves dividing fractional measurements.
- Construction and Engineering: Dividing fractional lengths and measurements is essential for accurate planning and execution.
- Data Analysis and Statistics: Many statistical calculations involve fractions and their division.
Conclusion: Mastering Fraction Division
Dividing fractions, especially when dealing with mixed numbers, may initially seem challenging. However, by mastering the fundamental concepts, including converting mixed numbers to improper fractions and utilizing the reciprocal method, you can confidently tackle a wide range of fraction division problems. Remember to always pay careful attention to the problem statement and use appropriate precision to avoid ambiguity and inaccuracies. The more you practice, the more intuitive this process will become. Proficiency in fraction division opens the door to a deeper understanding of mathematics and empowers you to solve problems across numerous disciplines.
Latest Posts
Latest Posts
-
1 5 To The Power Of 5
May 24, 2025
-
30 Days After August 16 2024
May 24, 2025
-
65 An Hour Is How Much A Year After Taxes
May 24, 2025
-
If You Are Born In 1999 How Old Are You
May 24, 2025
-
What Is The Greatest Common Factor Of 60 And 100
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 8 Divided By 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.