What Is 1/5 Divided By 1/2
listenit
May 12, 2025 · 5 min read
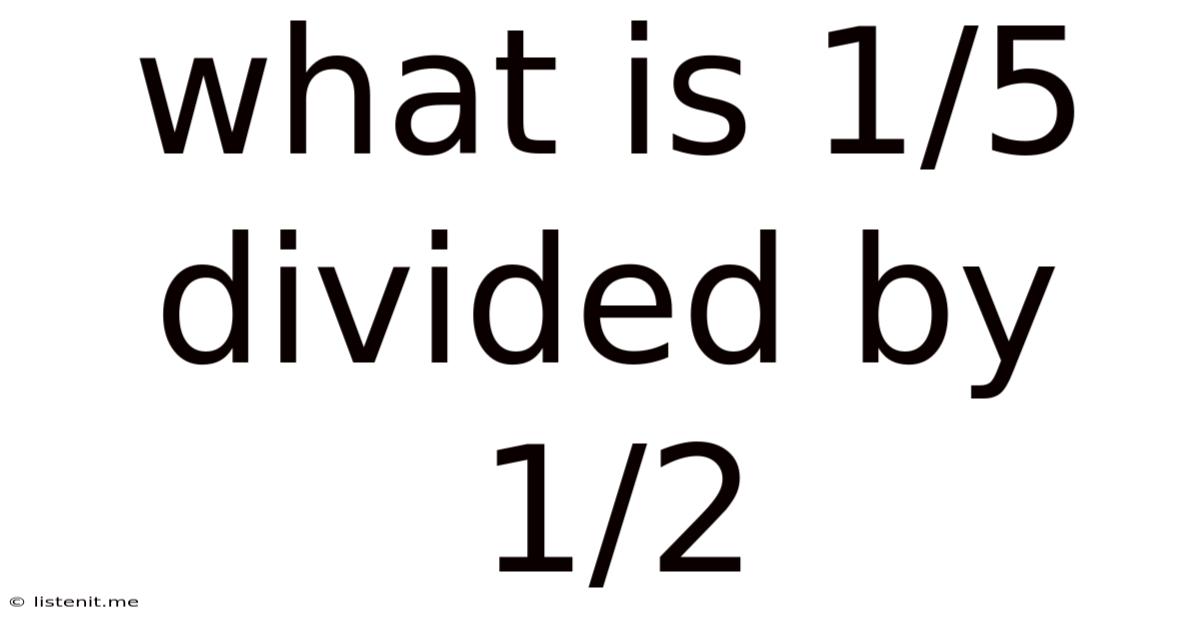
Table of Contents
What is 1/5 Divided by 1/2? A Deep Dive into Fraction Division
This seemingly simple math problem, "What is 1/5 divided by 1/2?", hides a wealth of mathematical concepts crucial for a strong foundation in arithmetic. This article will not only solve the problem but also delve into the why behind the solution, exploring different methods, and providing a comprehensive understanding of fraction division. We'll also touch on the practical applications of this fundamental concept.
Understanding Fraction Division: Beyond the Algorithm
Before tackling the specific problem, let's lay a solid groundwork. Dividing fractions isn't simply about memorizing a formula; it's about grasping the underlying mathematical principles. What does it mean to divide one fraction by another?
Imagine you have 1/5 of a pizza. Dividing this by 1/2 asks: "How many pieces of size 1/2 can you get from 1/5?" Clearly, you won't get a whole piece. This intuitive understanding helps visualize the process.
The "Keep, Change, Flip" Method
This popular mnemonic is a shortcut to the formal algorithm. It states: Keep the first fraction, change the division sign to multiplication, and flip (find the reciprocal of) the second fraction.
Applying this to our problem:
1/5 ÷ 1/2 = 1/5 x 2/1 = 2/5
So, you can get 2/5 of a half-sized pizza from a 1/5 slice. While this method works, it's important to understand why it works.
The Formal Algorithm: Reciprocals and Multiplication
The "Keep, Change, Flip" method is a streamlined version of a more formal approach involving reciprocals. The reciprocal of a fraction is obtained by swapping its numerator and denominator. For example, the reciprocal of 1/2 is 2/1 (or simply 2).
Dividing by a fraction is equivalent to multiplying by its reciprocal. This is the fundamental principle behind the "Keep, Change, Flip" method. Mathematically:
a/b ÷ c/d = a/b x d/c
Applying this to our problem:
1/5 ÷ 1/2 = 1/5 x 2/1 = 2/5
This formal approach highlights the mathematical reasoning behind the shortcut. It's not just a trick; it's a direct consequence of the definition of division and reciprocals.
Visualizing the Solution: A Geometric Approach
Let's visualize the problem using a geometric representation. Imagine a rectangle representing one whole unit.
- 1/5: Divide the rectangle into five equal parts. One of these parts represents 1/5.
- 1/2: Now, consider a piece that is half the size of the whole rectangle.
- Dividing 1/5 by 1/2: How many 1/2 sized pieces fit into the 1/5 piece?
If you carefully analyze the visualization, you'll see that two 1/5 pieces would make up one 1/2 piece. Therefore, 1/5 divided by 1/2 results in 2/5. This visual approach strengthens the intuitive understanding of fraction division.
Solving Similar Problems: Building Proficiency
Let's reinforce our understanding by tackling some similar problems:
Example 1: 2/3 ÷ 1/4
Applying the "Keep, Change, Flip" method:
2/3 ÷ 1/4 = 2/3 x 4/1 = 8/3 or 2 2/3
Example 2: 3/4 ÷ 2/5
Applying the "Keep, Change, Flip" method:
3/4 ÷ 2/5 = 3/4 x 5/2 = 15/8 or 1 7/8
Example 3: 1/7 ÷ 2/3
Applying the "Keep, Change, Flip" method:
1/7 ÷ 2/3 = 1/7 x 3/2 = 3/14
These examples demonstrate the consistent application of the method and the formal algorithm. Remember, practice is key to mastering fraction division.
Real-World Applications: Fractions in Everyday Life
Fraction division isn't confined to the classroom; it's relevant to numerous real-world scenarios:
- Cooking: Scaling down recipes often involves dividing fractions. If a recipe calls for 2/3 cup of flour and you want to make half the recipe, you'll need to divide 2/3 by 2.
- Sewing: Cutting fabric requires precise measurements. Dividing fractions is essential for accurately calculating material needs.
- Construction: Dividing fractions is crucial in many construction projects, for example, when calculating the amount of material needed to cover a certain area.
- Engineering: Engineers regularly utilize fraction division for precise calculations related to size, weight, and material usage.
These examples illustrate that understanding fraction division enhances practical problem-solving skills in various fields.
Advanced Concepts: Complex Fractions and Beyond
The principles of fraction division extend to more complex scenarios, such as dividing complex fractions (fractions containing fractions). These scenarios build upon the foundational concepts discussed above, requiring careful application of the order of operations and the rules of fraction manipulation.
For example, consider this complex fraction:
(1/2 + 1/3) ÷ (1/4 - 1/5)
Solving this involves:
- Simplifying the numerator (1/2 + 1/3 = 5/6)
- Simplifying the denominator (1/4 - 1/5 = 1/20)
- Dividing the simplified numerator by the simplified denominator (5/6 ÷ 1/20 = 5/6 x 20/1 = 100/6 = 50/3 or 16 2/3)
Mastering basic fraction division provides a solid foundation for tackling more complex mathematical challenges.
Conclusion: Mastering the Fundamentals
Understanding "What is 1/5 divided by 1/2?" goes beyond simply obtaining the answer (2/5). It's about grasping the underlying principles of fraction division, including the use of reciprocals, the formal algorithm, and the intuitive geometric representation. By practicing these methods and exploring real-world applications, you’ll not only master fraction division but also strengthen your overall mathematical proficiency, opening doors to more advanced mathematical concepts. Remember, consistent practice and a deep understanding of the "why" behind the methods are crucial for true mastery.
Latest Posts
Latest Posts
-
Simplify The Square Root Of 81
May 12, 2025
-
How Do Isotopes Of A Given Element Differ
May 12, 2025
-
What Is The Prime Factorization Of 726
May 12, 2025
-
Unit Vector Orthogonal To Two Vectors
May 12, 2025
-
Do Polar Molecules Need A Transport Protein
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/5 Divided By 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.