What Is 1 4 Plus 1 8
listenit
May 24, 2025 · 5 min read
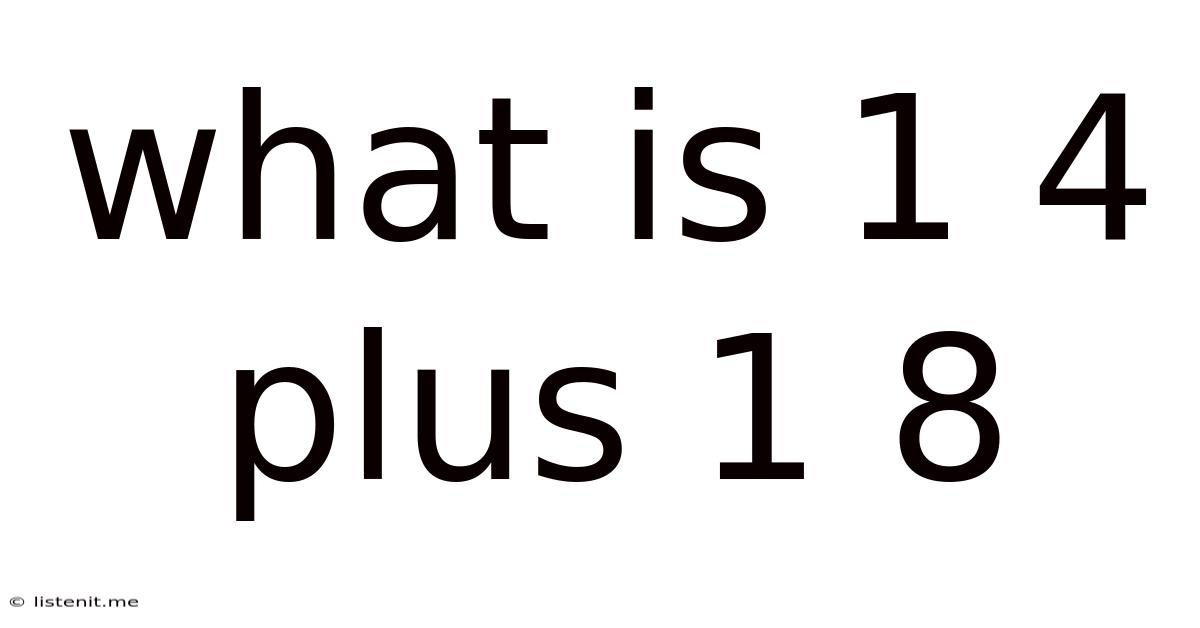
Table of Contents
What is 1/4 Plus 1/8? A Deep Dive into Fraction Addition
This seemingly simple question, "What is 1/4 plus 1/8?", opens the door to a world of mathematical concepts crucial for everyday life and advanced studies. While the answer itself is straightforward, exploring the methods and underlying principles involved provides a valuable understanding of fractions and their manipulation. This article will not only answer the question but will also delve into the various approaches to solving it, offering insights into the broader field of arithmetic and its applications.
Understanding Fractions: The Building Blocks
Before tackling the addition, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 1/4 (one-quarter), the numerator (1) tells us we have one part, and the denominator (4) tells us the whole is divided into four equal parts. Similarly, 1/8 (one-eighth) represents one part out of eight equal parts.
Method 1: Finding a Common Denominator
The most common and fundamental method for adding fractions involves finding a common denominator. This means converting the fractions so they share the same denominator before adding the numerators.
-
Identify the denominators: In our problem, the denominators are 4 and 8.
-
Find the least common multiple (LCM): The LCM is the smallest number that is a multiple of both denominators. In this case, the LCM of 4 and 8 is 8. This is because 8 is a multiple of 4 (4 x 2 = 8).
-
Convert the fractions: We need to convert 1/4 to an equivalent fraction with a denominator of 8. To do this, we multiply both the numerator and the denominator by 2:
(1 x 2) / (4 x 2) = 2/8
-
Add the fractions: Now that both fractions have the same denominator, we can add the numerators:
2/8 + 1/8 = (2 + 1) / 8 = 3/8
Therefore, 1/4 + 1/8 = 3/8.
Method 2: Visual Representation – A Pie Chart Approach
Visualizing fractions can significantly enhance understanding. Let's represent this addition using pie charts:
-
Imagine a pie cut into four equal slices (representing 1/4). One slice represents 1/4.
-
Now, imagine another pie cut into eight equal slices (representing 1/8). One slice represents 1/8.
-
To add 1/4 and 1/8, we need to find a way to compare these slices. We can see that two 1/8 slices equal one 1/4 slice.
-
Combining one 1/4 slice (equivalent to 2/8) and one 1/8 slice gives us a total of three 1/8 slices.
-
Therefore, 1/4 + 1/8 = 3/8
This visual method provides an intuitive understanding of the addition process, particularly beneficial for beginners.
Method 3: Using Decimal Equivalents
While not always the preferred method for fractions, converting to decimals can sometimes simplify the calculation.
-
Convert fractions to decimals:
1/4 = 0.25 1/8 = 0.125
-
Add the decimals:
0.25 + 0.125 = 0.375
-
Convert back to a fraction (if needed): 0.375 can be converted back to a fraction by recognizing it as 375/1000. Simplifying this fraction by dividing both numerator and denominator by 125 gives us 3/8.
Therefore, 1/4 + 1/8 = 3/8.
Beyond the Basics: Extending the Concept
The addition of 1/4 and 1/8 serves as a fundamental building block for more complex fraction operations. Understanding this simple addition lays the groundwork for tackling more challenging problems involving:
-
Adding multiple fractions: The same principle of finding a common denominator applies when adding more than two fractions. For example, 1/2 + 1/4 + 1/8 would involve finding the LCM of 2, 4, and 8, which is 8.
-
Subtracting fractions: Subtraction of fractions follows a similar process, requiring a common denominator before subtracting the numerators.
-
Multiplying and dividing fractions: These operations involve different rules, but mastering fraction addition is crucial for understanding the relationships between these operations.
-
Solving equations with fractions: Many algebraic equations involve fractions, and the ability to manipulate fractions is essential for solving these equations.
Real-World Applications: Where Fractions Matter
Fractions are not just abstract mathematical concepts; they are essential tools used extensively in everyday life and various professions. Some common examples include:
-
Cooking and baking: Recipes frequently involve fractions (e.g., 1/2 cup of sugar, 1/4 teaspoon of salt).
-
Construction and engineering: Precise measurements and calculations in construction and engineering often involve fractions and decimals.
-
Finance: Understanding fractions is crucial for dealing with percentages, interest rates, and other financial calculations.
-
Data analysis: Many datasets involve fractions and percentages, necessitating the ability to manipulate and interpret these values.
-
Science: Scientific measurements and calculations frequently utilize fractions and decimals for precise representation.
Mastering Fractions: Tips and Practice
Becoming proficient in fraction arithmetic requires consistent practice and a solid understanding of the underlying principles. Here are some helpful tips:
-
Practice regularly: The more you practice, the more comfortable and confident you'll become with fraction operations.
-
Visualize: Use visual aids like pie charts or diagrams to understand fraction concepts.
-
Break down problems: Complex problems can be broken down into smaller, more manageable steps.
-
Check your work: Always double-check your calculations to ensure accuracy.
-
Seek help when needed: Don't hesitate to ask for help from teachers, tutors, or online resources if you're struggling.
Conclusion: The Power of Understanding Fractions
The seemingly simple question, "What is 1/4 plus 1/8?", has led us on a journey through the fascinating world of fractions. While the answer, 3/8, is straightforward, understanding the methods and underlying principles involved empowers us to tackle more complex mathematical challenges and apply these skills to a wide range of real-world situations. Mastering fractions is not just about solving arithmetic problems; it's about developing a crucial skillset for success in various academic and professional endeavors. The journey of learning never ends, and continued exploration of mathematical concepts will only enhance your understanding and abilities. Remember that practice and perseverance are key to mastering any mathematical concept, including the manipulation of fractions.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 24 And 44
May 24, 2025
-
How Many Days Are There In 3 Years
May 24, 2025
-
11 00 An Hour Is How Much A Month
May 24, 2025
-
What Is The Greatest Common Factor Of 28 And 72
May 24, 2025
-
Round 6 38 To The Nearest Whole Number
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 4 Plus 1 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.