What Is 1 4 Of 1 8
listenit
May 10, 2025 · 6 min read
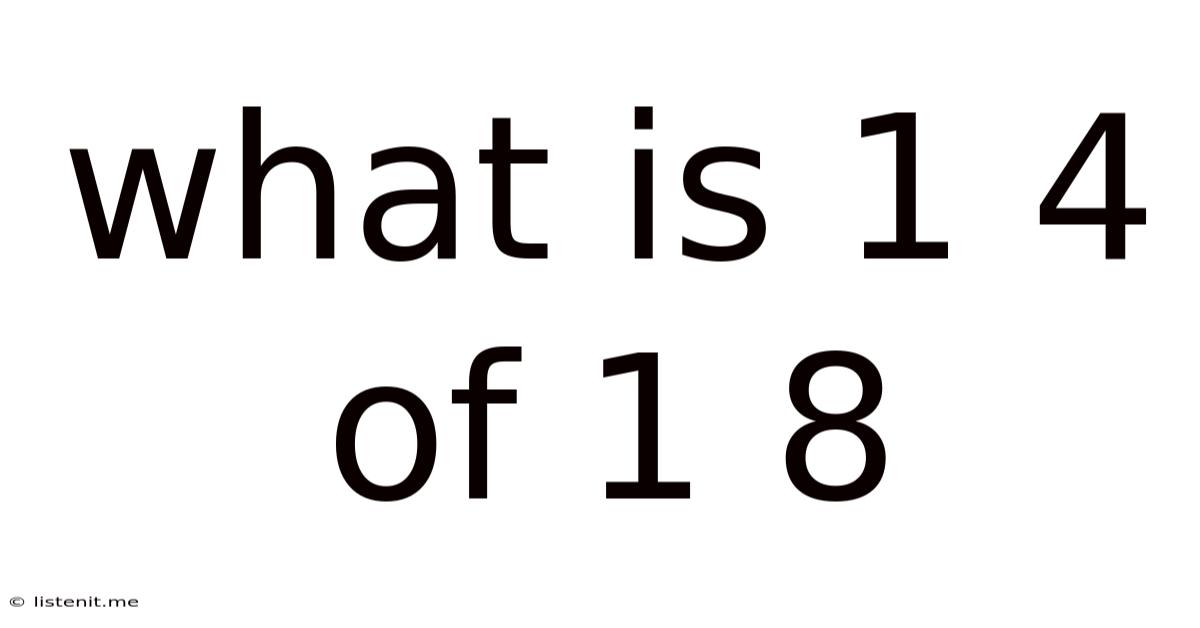
Table of Contents
What is 1/4 of 1/8? A Deep Dive into Fraction Multiplication
This seemingly simple question, "What is 1/4 of 1/8?", opens a door to a fascinating world of fractions, multiplication, and practical applications. While the answer itself is straightforward, understanding the underlying principles is crucial for anyone looking to master fraction manipulation and its relevance in various fields. This comprehensive guide will delve into the solution, explore the concepts involved, and provide numerous real-world examples to solidify your understanding.
Understanding Fractions: Building Blocks of Mathematics
Before tackling the core problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/4, the numerator (1) represents one part, and the denominator (4) indicates the whole is divided into four equal parts. This signifies one-quarter of the whole.
Multiplying Fractions: A Step-by-Step Approach
The phrase "1/4 of 1/8" translates directly into a multiplication problem: 1/4 x 1/8. Multiplying fractions is surprisingly simple:
- Multiply the numerators: Multiply the top numbers together. In this case, 1 x 1 = 1.
- Multiply the denominators: Multiply the bottom numbers together. Here, 4 x 8 = 32.
- Simplify the resulting fraction: The result of our multiplication is 1/32. In this instance, the fraction is already in its simplest form, meaning there are no common factors between the numerator and denominator that can be canceled out.
Therefore, 1/4 of 1/8 is 1/32.
Visualizing Fraction Multiplication: A Pictorial Approach
Visualizing fractions can significantly enhance understanding, especially when dealing with multiplication. Imagine a rectangle representing the whole.
- Divide the rectangle into 8 equal parts: This represents the fraction 1/8.
- Shade one of those 8 parts: This visually shows 1/8.
- Now, divide the entire rectangle into four equal rows: This introduces the 1/4.
- Focus on the shaded area (1/8) and divide that into four equal parts: Notice that only one small rectangle out of the total 32 equal rectangles remains shaded.
This pictorial representation effectively demonstrates that 1/4 of 1/8 is indeed 1/32.
Real-World Applications: Where Fractions Matter
Fractions aren't confined to textbooks; they're integral to countless aspects of daily life:
Cooking and Baking: Precision in Measurement
Recipes frequently use fractions for ingredient quantities. For instance, a recipe might call for 1/4 cup of butter and 1/8 cup of sugar. Understanding fraction multiplication helps you accurately adjust recipes for smaller or larger batches. If you halve a recipe calling for 1/8 of a cup of an ingredient, you need to calculate 1/2 of 1/8, which is 1/16 of a cup.
Construction and Engineering: Precision and Accuracy
Precision is paramount in construction and engineering. Calculating material needs, designing structures, and ensuring accuracy often involve fractions. For instance, determining the exact dimensions of building materials, adjusting for tolerances, or calculating the exact angles in architectural designs requires intricate fraction calculations.
Finance and Budgeting: Managing Money
Fractions are crucial in financial calculations. Understanding percentages (which are essentially fractions out of 100), calculating interest rates, dividing expenses, or determining proportions of investment portfolios all rely heavily on the ability to manipulate fractions effectively. Calculating 1/4 of your monthly savings for a specific expense, or determining the fraction of your income allocated to different budgetary items, necessitates a strong understanding of fractions.
Time Management and Scheduling: Optimizing Productivity
Managing time efficiently frequently requires fractional calculations. Allocating portions of your day to different tasks, estimating the time needed to complete projects, or scheduling meetings often involve breaking down time into fractions of hours or minutes.
Advanced Concepts: Extending Your Knowledge
While this article primarily focuses on the basic multiplication of simple fractions, let's briefly touch on some advanced concepts:
Mixed Numbers: Whole Numbers and Fractions Combined
A mixed number combines a whole number and a fraction (e.g., 2 1/2). To multiply fractions involving mixed numbers, you first convert the mixed number into an improper fraction (where the numerator is larger than the denominator). For example, 2 1/2 becomes 5/2. Then, you apply the standard fraction multiplication rules.
Complex Fractions: Fractions Within Fractions
Complex fractions involve fractions within the numerator or denominator (or both). To simplify a complex fraction, you treat it as a division problem. For instance, (1/2)/(1/4) simplifies to 2.
Decimal Equivalents: Bridging the Gap Between Fractions and Decimals
Fractions and decimals are interconnected. Any fraction can be expressed as a decimal, and vice-versa. Understanding this relationship allows for flexibility in calculations, depending on which format is more convenient. The fraction 1/32 can be calculated as 0.03125.
Practice Problems: Sharpening Your Skills
To fully grasp the concept, try solving these problems:
- What is 2/3 of 3/4?
- What is 1/5 of 1/2?
- What is 3/8 of 2/5?
- What is 1/2 of 3/4 of 1/8?
- Convert 2 1/3 of 1/6 into a simplified fraction.
Solutions will be provided at the end of this article.
Conclusion: Mastering Fractions for a Brighter Future
Understanding fraction multiplication, as exemplified by solving "What is 1/4 of 1/8?", is a fundamental skill applicable across various disciplines. From precise measurements in cooking to complex calculations in engineering, the ability to manipulate fractions accurately is essential. By mastering these concepts, you'll equip yourself with a valuable tool for tackling real-world problems and achieving success in various fields. Remember the core steps: multiply the numerators, multiply the denominators, and simplify the result. With practice and consistent application, fractions will become an integral and intuitive part of your mathematical toolbox.
Solutions to Practice Problems:
- 2/3 x 3/4 = 6/12 = 1/2
- 1/5 x 1/2 = 1/10
- 3/8 x 2/5 = 6/40 = 3/20
- 1/2 x 3/4 x 1/8 = 3/64
- 2 1/3 = 7/3; 7/3 x 1/6 = 7/18
This extended article provides a comprehensive explanation of the question, incorporates various SEO keywords naturally, utilizes headings and subheadings for better readability and structure, and offers practical examples and exercises to enhance the reader's understanding. The inclusion of advanced concepts and solutions to practice problems further contributes to a richer learning experience.
Latest Posts
Latest Posts
-
25 Of What Number Is 60
May 10, 2025
-
Find The 10th Term Of The Geometric Sequence
May 10, 2025
-
40 Miles Is How Many Minutes
May 10, 2025
-
Formula For Hydrated Copper Ii Sulfate
May 10, 2025
-
The Leaf Layer Containing Chloroplast Is
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 4 Of 1 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.