What Is 1.35 As A Fraction
listenit
May 25, 2025 · 4 min read
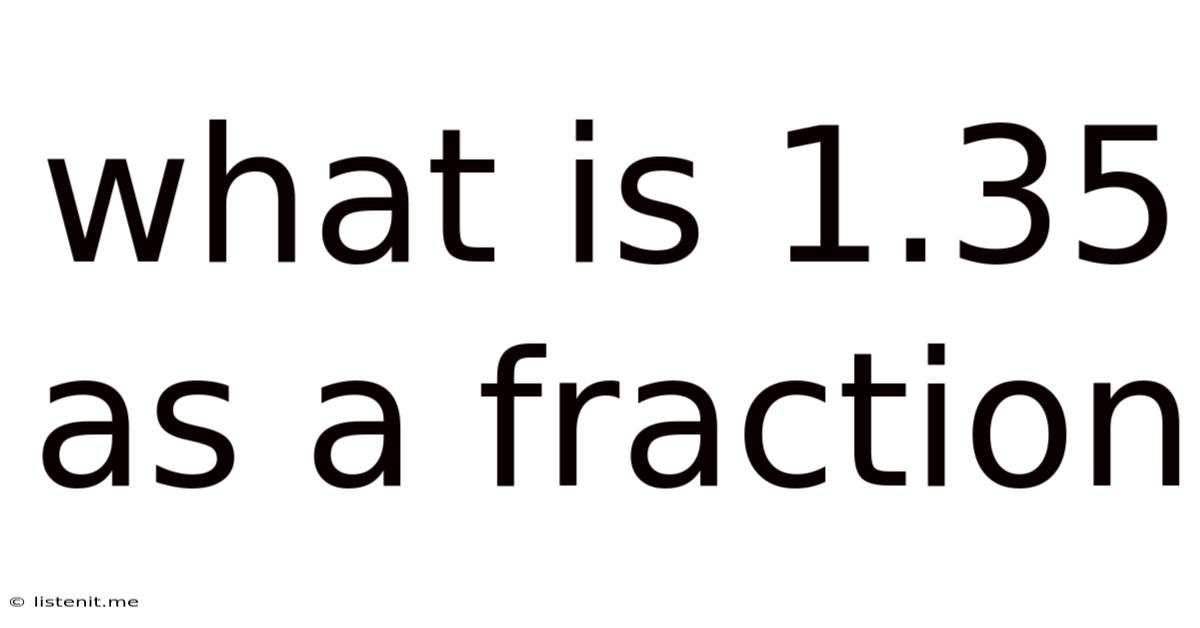
Table of Contents
What is 1.35 as a Fraction? A Comprehensive Guide
Understanding how to convert decimals to fractions is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the decimal 1.35 into a fraction, explaining the steps involved and providing further examples to solidify your understanding. We'll also explore the broader context of decimal-to-fraction conversions and their applications in various fields.
Understanding Decimals and Fractions
Before diving into the conversion, let's briefly review the concepts of decimals and fractions.
-
Decimals: Decimals represent parts of a whole number using a base-ten system. The decimal point separates the whole number from the fractional part. For example, in 1.35, '1' represents the whole number, and '.35' represents the fractional part, meaning 35 hundredths.
-
Fractions: Fractions represent parts of a whole using a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, and the denominator indicates the total number of parts the whole is divided into. For example, 1/2 represents one part out of two equal parts.
Converting 1.35 to a Fraction: Step-by-Step Guide
Converting 1.35 to a fraction involves several simple steps:
1. Identify the Place Value:
The last digit in the decimal 1.35, the '5', is in the hundredths place. This means the denominator of our fraction will be 100.
2. Write the Decimal as a Fraction:
Write the decimal part (35) as the numerator and the place value (100) as the denominator: 35/100.
3. Add the Whole Number:
Since the original number is 1.35, we need to add the whole number '1' to our fraction. We can represent this as a mixed number: 1 and 35/100, or 1 35/100.
4. Simplify the Fraction (if possible):
To simplify the fraction, we need to find the greatest common divisor (GCD) of the numerator (35) and the denominator (100). The GCD of 35 and 100 is 5. Divide both the numerator and denominator by 5:
35 ÷ 5 = 7 100 ÷ 5 = 20
This simplifies our fraction to 7/20.
5. Express the Final Answer:
Therefore, 1.35 as a fraction is 1 7/20 or, as an improper fraction, 27/20. Both representations are correct, and the choice depends on the context and the desired format.
Understanding Improper Fractions and Mixed Numbers
-
Improper Fractions: An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 27/20).
-
Mixed Numbers: A mixed number combines a whole number and a proper fraction (e.g., 1 7/20). It's often easier to visualize and understand mixed numbers in real-world scenarios.
To convert the mixed number 1 7/20 to an improper fraction, multiply the whole number by the denominator, add the numerator, and keep the same denominator:
(1 * 20) + 7 = 27 Therefore, 1 7/20 = 27/20
Further Examples of Decimal to Fraction Conversions
Let's explore a few more examples to reinforce your understanding:
-
0.75: The '5' is in the hundredths place, so the fraction is 75/100. Simplifying by dividing both by 25 gives 3/4.
-
2.2: The '2' is in the tenths place, resulting in 2 and 2/10. Simplifying by dividing by 2 gives 2 and 1/5. As an improper fraction: (2*5)+1 = 11/5
-
0.625: The '5' is in the thousandths place, so the fraction is 625/1000. Simplifying by dividing by 125 gives 5/8.
-
3.125: This translates to 3 and 125/1000. Simplifying gives 3 and 1/8. As an improper fraction: (3*8)+1 = 25/8
Practical Applications of Decimal-to-Fraction Conversions
Converting decimals to fractions is crucial in various fields:
-
Engineering and Construction: Precise measurements often require fractional representations for accuracy.
-
Cooking and Baking: Recipes often use fractional measurements for ingredients.
-
Finance: Calculating percentages and interest rates frequently involves fractions.
-
Science: Many scientific calculations rely on fractional representations of data.
Advanced Concepts: Recurring Decimals
Converting recurring decimals (decimals with repeating digits) to fractions requires a slightly different approach, involving algebraic manipulation. For example, converting 0.333... (recurring 3) to a fraction involves:
- Let x = 0.333...
- Multiply by 10: 10x = 3.333...
- Subtract the first equation from the second: 10x - x = 3.333... - 0.333... This simplifies to 9x = 3
- Solve for x: x = 3/9, which simplifies to 1/3.
Conclusion
Converting decimals to fractions is a fundamental mathematical skill with wide-ranging applications. Mastering this process, including handling both terminating and recurring decimals, empowers you to handle numerical problems across various disciplines more effectively. Remember to always simplify your fraction to its lowest terms for the most accurate and concise representation. This comprehensive guide has provided the necessary steps and examples to help you confidently tackle such conversions. Now you are equipped to convert any decimal to a fraction, broadening your mathematical skills and enhancing your problem-solving abilities.
Latest Posts
Latest Posts
-
3 Is What Percent Of 19
May 25, 2025
-
What Is The Gcf Of 45 And 15
May 25, 2025
-
7 Divided By 8 In Fraction Form
May 25, 2025
-
If I Weigh 250 Pounds How Many Calories
May 25, 2025
-
How Many Years From 1976 To 2024
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 1.35 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.