What Is 1 2 X 1 3
listenit
May 11, 2025 · 6 min read
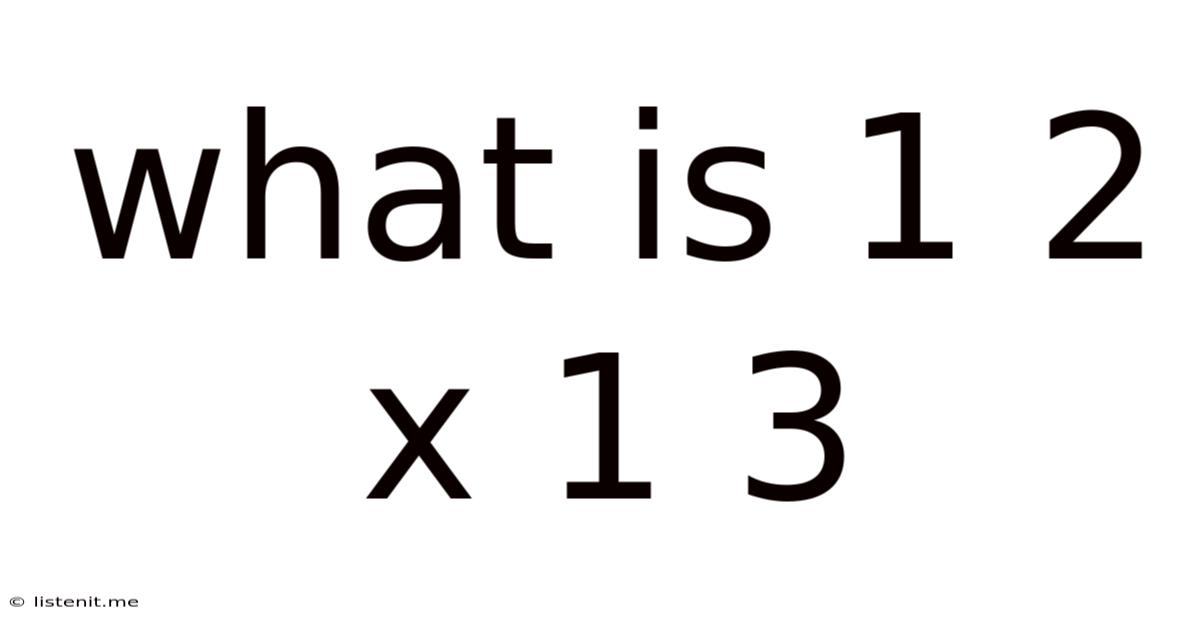
Table of Contents
What is 1/2 x 1/3? A Deep Dive into Fraction Multiplication
Understanding fractions is fundamental to mathematics, and mastering fraction multiplication is a crucial stepping stone to more advanced concepts. This seemingly simple question, "What is 1/2 x 1/3?", opens a door to a deeper understanding of fractions, their representation, and their practical applications in everyday life. This comprehensive guide will not only answer the question but also delve into the mechanics of fraction multiplication, offering various approaches and illustrative examples to solidify your comprehension.
Understanding Fractions: A Quick Recap
Before diving into multiplication, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) signifies one part, and the denominator (2) signifies that the whole is divided into two equal parts. Similarly, 1/3 represents one part of a whole divided into three equal parts.
Multiplying Fractions: The Straightforward Approach
Multiplying fractions is surprisingly straightforward. The process involves two simple steps:
- Multiply the numerators: Multiply the top numbers of both fractions together.
- Multiply the denominators: Multiply the bottom numbers of both fractions together.
Let's apply this to our question: What is 1/2 x 1/3?
- Multiply the numerators: 1 x 1 = 1
- Multiply the denominators: 2 x 3 = 6
Therefore, 1/2 x 1/3 = 1/6.
Visualizing Fraction Multiplication
Visual aids can significantly enhance the understanding of abstract mathematical concepts. Let's visualize 1/2 x 1/3 using a diagram:
Imagine a rectangle representing a whole. Divide this rectangle into three equal columns (representing the denominator of 1/3). Now, shade one of these columns to represent 1/3.
Next, divide the entire rectangle into two equal rows (representing the denominator of 1/2). You'll notice that the rectangle is now divided into six equal smaller rectangles (2 x 3 = 6).
Finally, focus on the area where the shaded column (1/3) intersects with one of the rows (1/2). This overlapping area represents 1/6 of the whole rectangle. This visually demonstrates that 1/2 x 1/3 = 1/6.
Exploring Different Approaches: The "Of" Interpretation
Instead of directly thinking of multiplication as a purely arithmetic operation, consider the word "of" as an alternative interpretation. "1/2 x 1/3" can be read as "1/2 of 1/3".
This perspective allows for a slightly different approach to understanding the multiplication. It means we are finding one-half of one-third. If you had a pizza sliced into three equal pieces, and you wanted to find half of one of those slices, you would effectively have one-sixth of the whole pizza.
Practical Applications of Fraction Multiplication
Fraction multiplication is not confined to the realm of theoretical mathematics. It has numerous practical applications in daily life, including:
-
Cooking and Baking: Scaling recipes up or down requires multiplying fractions. For example, if a recipe calls for 1/2 cup of flour and you want to make half the recipe, you'll need to calculate 1/2 x 1/2 = 1/4 cup of flour.
-
Construction and Engineering: Calculating dimensions and material quantities often involves multiplying fractions. For instance, determining the area of a rectangular surface might involve multiplying fractional lengths and widths.
-
Finance and Budgeting: Calculating percentages, interest rates, and portions of a budget can frequently involve fraction multiplication.
-
Time Management: Dividing tasks and scheduling activities often utilizes fraction multiplication. For example, calculating how much time you’ll spend on a project that requires 1/3 of your workday.
Beyond the Basics: Multiplying More Than Two Fractions
The principles of fraction multiplication extend seamlessly to multiplying more than two fractions. The process remains the same:
- Multiply all the numerators together.
- Multiply all the denominators together.
For example, to solve 1/2 x 1/3 x 1/4:
- Multiply numerators: 1 x 1 x 1 = 1
- Multiply denominators: 2 x 3 x 4 = 24
Therefore, 1/2 x 1/3 x 1/4 = 1/24.
Simplifying Fractions: A Crucial Step
After multiplying fractions, it's often necessary to simplify the resulting fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by the GCD.
For instance, if the result of a fraction multiplication is 4/8, the GCD of 4 and 8 is 4. Dividing both the numerator and denominator by 4 simplifies the fraction to 1/2.
Simplifying fractions ensures that your answer is presented in its most concise and understandable form.
Mixed Numbers and Fraction Multiplication
Mixed numbers, which combine a whole number and a fraction (e.g., 1 1/2), require an extra step before multiplication. First, convert the mixed number into an improper fraction. An improper fraction has a numerator larger than its denominator.
To convert a mixed number to an improper fraction, multiply the whole number by the denominator, add the numerator, and place the result over the original denominator.
For example, to convert 1 1/2 to an improper fraction:
- Multiply the whole number (1) by the denominator (2): 1 x 2 = 2
- Add the numerator (1): 2 + 1 = 3
- Place the result over the original denominator (2): 3/2
Now you can multiply the improper fraction as you would any other fraction.
Fraction Multiplication and Decimals: Interconversion
Fractions and decimals are interchangeable representations of parts of a whole. You can convert a fraction to a decimal by dividing the numerator by the denominator. Conversely, you can convert a decimal to a fraction by writing the decimal as a fraction over a power of 10 and simplifying.
For example, 1/2 can be converted to a decimal by dividing 1 by 2, resulting in 0.5. Similarly, 0.75 can be converted to a fraction as 75/100, which simplifies to 3/4.
Being able to easily interconvert between fractions and decimals provides flexibility in solving problems and choosing the most convenient representation.
Error Analysis and Common Mistakes
Even with the straightforward process, common mistakes can arise when multiplying fractions:
- Forgetting to multiply both the numerators and denominators: Remember that both the top and bottom numbers need to be multiplied.
- Improper simplification: Ensure you find the greatest common divisor to simplify to the lowest terms.
- Errors in converting mixed numbers: Double-check your calculations when converting mixed numbers to improper fractions.
Paying close attention to detail and practicing regularly helps minimize these errors.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication is essential for success in various aspects of life, not just mathematics. This deep dive into the topic has covered the fundamental principles, visualization techniques, real-world applications, and potential pitfalls. By understanding and applying these concepts, you can confidently tackle fraction multiplication problems and use this knowledge to solve more complex mathematical challenges. Remember, consistent practice and attention to detail are key to building a solid understanding and achieving fluency. The seemingly simple question, "What is 1/2 x 1/3?", has now opened up a much broader and more comprehensive understanding of fractions and their power in the real world.
Latest Posts
Latest Posts
-
2 3 Cup Minus 1 2 Cup Equals
May 12, 2025
-
A Force Of Attraction Between Two Objects
May 12, 2025
-
What Is The Oxidation Number Of Fluorine
May 12, 2025
-
Molar Ratio Of Naoh And Hcl
May 12, 2025
-
What Is 1 3 Kg In Lbs
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 2 X 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.