What Is 1 2 Minus 1 3
listenit
Apr 07, 2025 · 5 min read
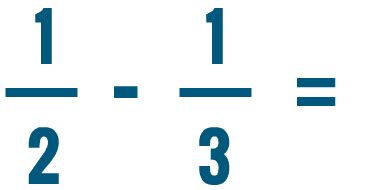
Table of Contents
What is 1/2 Minus 1/3? A Deep Dive into Fraction Subtraction
Understanding fractions is a fundamental skill in mathematics, crucial for various applications from baking to engineering. This seemingly simple question – "What is 1/2 minus 1/3?" – provides an excellent opportunity to explore the core concepts of fraction subtraction and delve into the underlying principles. This article will not only solve the equation but also explain the process in detail, offering various approaches to enhance your understanding and problem-solving abilities.
Understanding Fractions: A Quick Refresher
Before tackling the subtraction, let's review the basics of fractions. A fraction represents a part of a whole. It's composed of two parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating how many equal parts the whole is divided into.
For instance, in the fraction 1/2, the numerator (1) signifies we have one part, and the denominator (2) indicates the whole is divided into two equal parts. Therefore, 1/2 represents one-half.
Finding a Common Denominator: The Key to Fraction Subtraction
Unlike adding or subtracting whole numbers, we cannot directly subtract fractions with different denominators. The crucial step in subtracting (or adding) fractions is to find a common denominator. This is a number that is a multiple of both denominators. The common denominator allows us to express both fractions in terms of the same-sized pieces, enabling direct subtraction.
Let's consider our problem: 1/2 - 1/3. The denominators are 2 and 3. To find a common denominator, we look for the least common multiple (LCM) of 2 and 3.
The multiples of 2 are: 2, 4, 6, 8, 10... The multiples of 3 are: 3, 6, 9, 12...
The least common multiple of 2 and 3 is 6. Therefore, 6 is our common denominator.
Converting Fractions to a Common Denominator
Now that we have a common denominator (6), we need to convert both fractions, 1/2 and 1/3, to equivalent fractions with a denominator of 6. This is done by multiplying both the numerator and the denominator of each fraction by the appropriate factor.
For 1/2: To get a denominator of 6, we need to multiply the denominator (2) by 3. To maintain the value of the fraction, we must also multiply the numerator (1) by 3. This gives us:
(1 x 3) / (2 x 3) = 3/6
For 1/3: To get a denominator of 6, we need to multiply the denominator (3) by 2. Similarly, we multiply the numerator (1) by 2:
(1 x 2) / (3 x 2) = 2/6
Performing the Subtraction
Now that both fractions have the same denominator (6), we can perform the subtraction:
3/6 - 2/6
When subtracting fractions with the same denominator, we subtract the numerators and keep the denominator the same:
(3 - 2) / 6 = 1/6
Therefore, 1/2 - 1/3 = 1/6
Alternative Methods: Visual Representation and Real-World Examples
While the above method is the standard algebraic approach, let's explore alternative methods to solidify your understanding.
Visual Representation: Using Diagrams
Imagine a pizza cut into six slices. 1/2 of the pizza is 3 slices (3/6), and 1/3 of the pizza is 2 slices (2/6). If you take away 2 slices (1/3) from 3 slices (1/2), you are left with 1 slice (1/6). This visual representation can make the concept more intuitive.
Real-World Examples: Applying Fractions to Everyday Life
Fractions are ubiquitous in our daily lives. Consider baking a cake. If a recipe calls for 1/2 cup of sugar and 1/3 cup of butter, and you want to know the difference in quantity, you'd be performing the exact calculation: 1/2 - 1/3 = 1/6 cup.
Expanding on Fraction Subtraction: More Complex Scenarios
The principles discussed above extend to more complex fraction subtraction problems. Let's consider a few examples:
Example 1: Subtracting Fractions with Larger Numerators and Denominators
Let's subtract 7/12 from 5/6.
- Find the common denominator: The LCM of 6 and 12 is 12.
- Convert fractions: 5/6 = (5 x 2) / (6 x 2) = 10/12
- Subtract: 10/12 - 7/12 = 3/12
- Simplify: 3/12 can be simplified by dividing both numerator and denominator by 3, resulting in 1/4.
Example 2: Subtracting Mixed Numbers
A mixed number consists of a whole number and a fraction (e.g., 2 1/3). To subtract mixed numbers, you first convert them into improper fractions (where the numerator is larger than the denominator). Then, follow the steps for subtracting regular fractions.
Let's subtract 1 1/4 from 3 1/2:
- Convert to improper fractions: 3 1/2 = 7/2 and 1 1/4 = 5/4
- Find the common denominator: The LCM of 2 and 4 is 4.
- Convert fractions: 7/2 = (7 x 2) / (2 x 2) = 14/4
- Subtract: 14/4 - 5/4 = 9/4
- Convert back to a mixed number: 9/4 = 2 1/4
Troubleshooting Common Mistakes in Fraction Subtraction
Several common errors can arise when working with fraction subtraction. Awareness of these pitfalls can help you avoid them:
- Incorrectly finding the common denominator: Always double-check your LCM calculation.
- Forgetting to multiply both numerator and denominator: Remember that multiplying only the numerator or denominator changes the value of the fraction.
- Subtracting denominators: The denominator remains the same throughout the subtraction process.
- Not simplifying the result: Always simplify your final answer to its lowest terms.
Conclusion: Mastering Fraction Subtraction and Beyond
Mastering fraction subtraction is a cornerstone of mathematical proficiency. This article has provided a comprehensive guide, from the fundamental principles to tackling more complex problems. By understanding the concepts of common denominators, conversion, and simplification, you can confidently tackle any fraction subtraction challenge. Remember to practice regularly, utilize visual aids when necessary, and always double-check your work. With consistent effort, you'll become adept at this essential mathematical skill, opening doors to more advanced concepts and applications. The ability to confidently handle fractions paves the way for success in various mathematical fields, from algebra and calculus to data analysis and beyond. So keep practicing and enjoy the journey of exploring the fascinating world of numbers!
Latest Posts
Latest Posts
-
What Is The Difference Between Chemical And Nuclear Reactions
Apr 07, 2025
-
Balance The Equation Ch4 O2 Co2 H2o
Apr 07, 2025
-
Is Mg A Cation Or Anion
Apr 07, 2025
-
What Is One Half Of A Quart
Apr 07, 2025
-
The Atomic Number Is The Same As The Number Of
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 2 Minus 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.