What Is 1 2 Divided By 3 4
listenit
May 12, 2025 · 4 min read
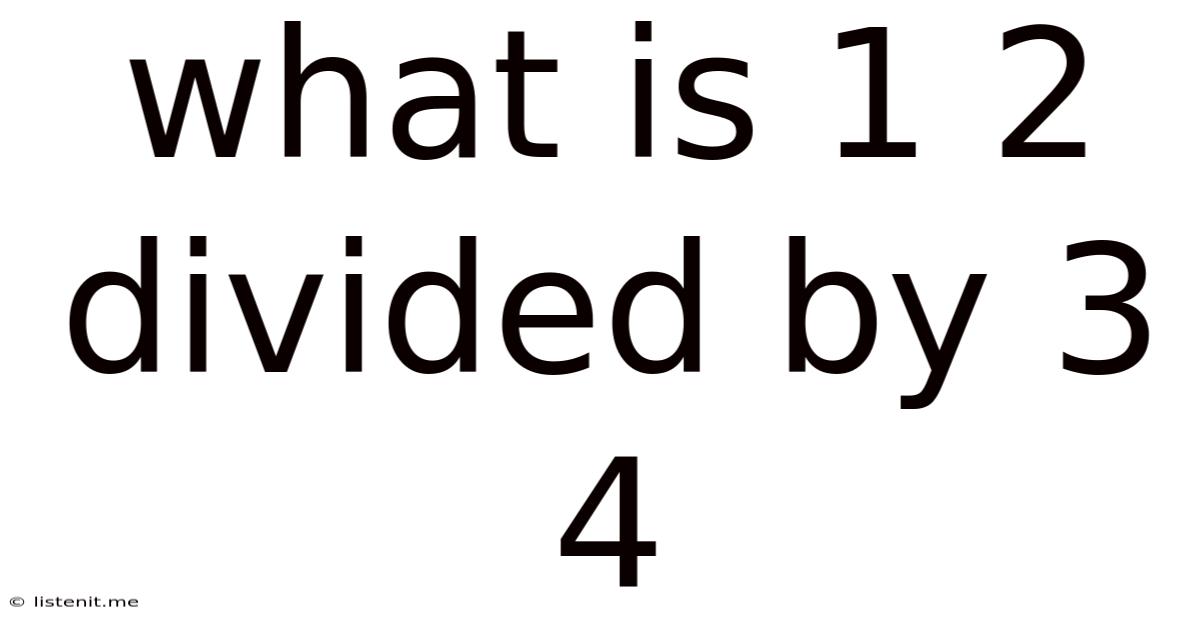
Table of Contents
What is 1 2/3 Divided by 3/4? A Comprehensive Guide to Fraction Division
Understanding fraction division can be tricky, but mastering it opens doors to solving a wide range of mathematical problems. This comprehensive guide will walk you through the process of dividing mixed numbers, specifically tackling the question: What is 1 2/3 divided by 3/4? We'll break down the steps, explain the underlying concepts, and provide you with practical tips and examples to solidify your understanding.
Understanding Mixed Numbers and Fractions
Before diving into the division, let's refresh our understanding of mixed numbers and fractions.
Mixed Numbers
A mixed number combines a whole number and a fraction. For example, 1 2/3 represents one whole unit plus two-thirds of another unit. To perform calculations, it's often easier to convert mixed numbers into improper fractions.
Improper Fractions
An improper fraction has a numerator (top number) that is greater than or equal to its denominator (bottom number). For example, 5/3 is an improper fraction. Converting a mixed number to an improper fraction involves multiplying the whole number by the denominator, adding the numerator, and keeping the same denominator.
Example: Converting 1 2/3 to an improper fraction:
- Multiply the whole number (1) by the denominator (3): 1 * 3 = 3
- Add the numerator (2): 3 + 2 = 5
- Keep the same denominator (3): 5/3
Therefore, 1 2/3 is equivalent to 5/3.
Dividing Fractions: The Reciprocal Method
The core principle of dividing fractions involves using the reciprocal of the second fraction. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 3/4 is 4/3.
To divide fractions, we follow these steps:
- Convert any mixed numbers to improper fractions. (As demonstrated above)
- Change the division sign to a multiplication sign.
- Replace the second fraction with its reciprocal.
- Multiply the numerators together.
- Multiply the denominators together.
- Simplify the resulting fraction, if possible.
Solving 1 2/3 Divided by 3/4
Now let's apply these steps to our problem: 1 2/3 ÷ 3/4
-
Convert 1 2/3 to an improper fraction: As shown earlier, 1 2/3 = 5/3
-
Rewrite the problem: 5/3 ÷ 3/4
-
Change the division sign to multiplication and use the reciprocal: 5/3 × 4/3
-
Multiply the numerators: 5 × 4 = 20
-
Multiply the denominators: 3 × 3 = 9
-
Simplify the resulting fraction: 20/9
The improper fraction 20/9 can be converted back into a mixed number:
- Divide the numerator (20) by the denominator (9): 20 ÷ 9 = 2 with a remainder of 2.
- The whole number is 2.
- The remainder (2) becomes the new numerator.
- The denominator remains the same (9).
Therefore, 20/9 = 2 2/9
Therefore, 1 2/3 divided by 3/4 equals 2 2/9.
Real-World Applications of Fraction Division
Understanding fraction division isn't just about solving textbook problems; it's a crucial skill applicable in various real-world scenarios:
-
Cooking and Baking: Many recipes require precise measurements. If a recipe calls for 2/3 cup of flour but you want to make only 3/4 of the recipe, you'll need to divide fractions to determine the correct amount of flour.
-
Construction and Engineering: Precise calculations are essential in construction and engineering projects. Dividing fractions helps determine material quantities, measurements, and proportions.
-
Sewing and Crafting: Tailoring and crafting projects frequently involve working with fractional measurements of fabric, yarn, or other materials. Accurate calculations are vital to ensure the project's success.
-
Financial Calculations: Fraction division plays a role in various financial calculations, including determining portions of investments, splitting bills, or calculating percentages.
Expanding Your Understanding: Further Exploration
While we've focused on dividing mixed numbers by fractions, the principles can be extended to other scenarios:
-
Dividing Fractions by Whole Numbers: Treat the whole number as a fraction with a denominator of 1 (e.g., 5 = 5/1). Then, follow the same reciprocal method.
-
Dividing Fractions by Other Fractions: The reciprocal method works consistently regardless of the type of fractions involved.
-
Complex Fractions: These involve fractions within fractions. To simplify complex fractions, treat them as division problems and apply the reciprocal method.
Mastering Fraction Division: Practice and Resources
The key to mastering fraction division is consistent practice. Work through various examples, starting with simpler problems and gradually increasing the complexity. Online resources, such as educational websites and math tutorials, can provide additional practice problems and explanations. Don't be afraid to seek help from teachers, tutors, or fellow students if you encounter difficulties. Consistent effort and practice will significantly improve your understanding and confidence in solving fraction division problems.
Conclusion: Building a Strong Foundation in Mathematics
Understanding fraction division is a fundamental building block in mathematics. It provides a solid foundation for tackling more complex mathematical concepts and problem-solving scenarios. By mastering the techniques and principles outlined in this guide, you'll not only be able to confidently solve problems like "What is 1 2/3 divided by 3/4?" but also apply this valuable skill to a wide range of real-world applications. Remember, consistent practice is key to building a strong foundation in mathematics and unlocking your full potential in this field.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1 2 Divided By 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.