What Is 1/2 + 3/8 In Fraction Form
listenit
May 12, 2025 · 5 min read
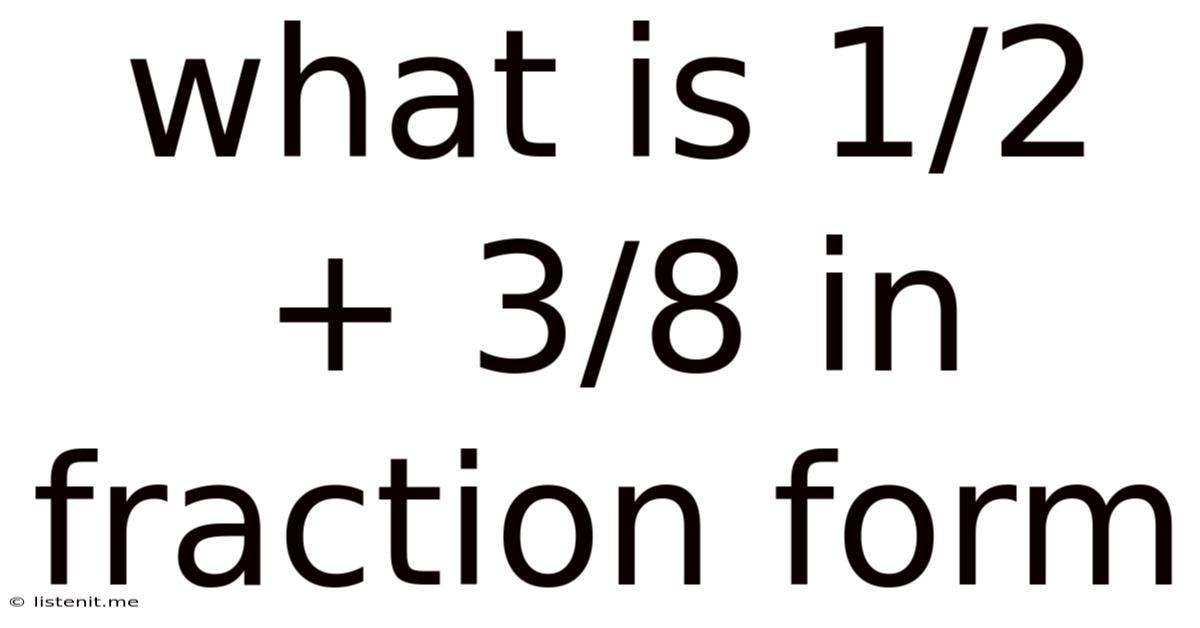
Table of Contents
What is 1/2 + 3/8 in Fraction Form? A Comprehensive Guide
Adding fractions might seem daunting at first, but with a clear understanding of the underlying principles, it becomes a straightforward process. This comprehensive guide will walk you through the steps of solving 1/2 + 3/8, explaining the concepts involved in a way that's easy to understand, regardless of your mathematical background. We'll also explore various methods and delve into related fraction operations to solidify your understanding.
Understanding the Basics of Fraction Addition
Before we tackle the specific problem of 1/2 + 3/8, let's review the fundamental concepts of fractions. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
To add or subtract fractions, a crucial concept is the common denominator. This is a number that is a multiple of both denominators. Why is this necessary? Imagine trying to add apples and oranges directly – it doesn't make sense unless you find a common unit of measurement. Similarly, you can't directly add fractions with different denominators.
Finding the Common Denominator
In our problem, 1/2 + 3/8, the denominators are 2 and 8. To find the common denominator, we look for the least common multiple (LCM) of 2 and 8. This is the smallest number that both 2 and 8 divide into evenly.
Several methods exist for finding the LCM:
-
Listing Multiples: List the multiples of each number until you find a common one. Multiples of 2: 2, 4, 6, 8, 10... Multiples of 8: 8, 16, 24... The least common multiple is 8.
-
Prime Factorization: Break down each number into its prime factors. 2 = 2 and 8 = 2 x 2 x 2. The LCM is formed by taking the highest power of each prime factor present: 2 x 2 x 2 = 8.
Therefore, our common denominator is 8.
Converting Fractions to a Common Denominator
Now that we have our common denominator (8), we need to convert both fractions so they have this denominator.
-
1/2: To change the denominator from 2 to 8, we multiply both the numerator and the denominator by 4 (because 8/2 = 4). This gives us (1 x 4) / (2 x 4) = 4/8. Notice that 4/8 is equivalent to 1/2; we've just changed its representation.
-
3/8: This fraction already has a denominator of 8, so it doesn't need to be changed.
Adding the Fractions
Now that both fractions have the same denominator, we can add them:
4/8 + 3/8 = (4 + 3) / 8 = 7/8
Therefore, 1/2 + 3/8 = 7/8
Simplifying Fractions (If Necessary)
In this case, 7/8 is already in its simplest form. A fraction is simplified when the numerator and denominator have no common factors other than 1. If we had obtained a fraction like 6/8, we could simplify it by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 2 in this case, resulting in 3/4.
Alternative Methods for Adding Fractions
While the method described above is the most common and generally recommended, other approaches exist, especially for more complex fraction addition problems.
-
Using a Calculator: Many calculators have fraction capabilities, allowing you to directly input the fractions and obtain the result. However, understanding the underlying process is crucial for developing a strong mathematical foundation.
-
Visual Representation: For simpler problems, visualizing the fractions using diagrams or shapes can be helpful. For example, you could represent 1/2 as half of a circle and 3/8 as three-eighths of a circle. Combining them visually would show that the total is 7/8 of the circle.
Further Exploration: Subtracting, Multiplying, and Dividing Fractions
The principles of finding a common denominator extend to subtracting fractions. The process is identical; you find the common denominator, convert the fractions, and then subtract the numerators.
Multiplying fractions is simpler; you multiply the numerators together and the denominators together. For example, (1/2) x (3/8) = (1 x 3) / (2 x 8) = 3/16.
Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying. For example, (1/2) ÷ (3/8) = (1/2) x (8/3) = 8/6 = 4/3.
Practical Applications of Fraction Addition
Understanding fraction addition isn't just an academic exercise; it has numerous real-world applications:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. Adding fractions helps accurately measure the required quantities.
-
Construction and Engineering: Precise measurements are vital in construction and engineering projects. Fraction addition is used to calculate dimensions and quantities.
-
Finance: Dealing with portions of money or shares often involves fraction addition and subtraction.
-
Data Analysis: When working with datasets, understanding fractions is helpful for interpreting proportions and percentages.
Conclusion
Adding fractions, such as 1/2 + 3/8, might seem intimidating initially, but by breaking down the problem into smaller, manageable steps, it becomes straightforward. Remember the importance of finding the common denominator, converting the fractions, and then adding (or subtracting) the numerators. Practicing these steps regularly will build your confidence and fluency in working with fractions, empowering you to tackle more complex mathematical problems. The principles of fraction addition are fundamental to numerous areas of life, making it a crucial skill to master. Understanding these concepts will not only help you solve mathematical problems but also enhance your problem-solving skills in various real-world scenarios. Remember to always simplify your answer to its lowest terms for the most accurate and concise representation of your solution.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1/2 + 3/8 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.