What Is 1.125 In A Fraction
listenit
May 21, 2025 · 5 min read
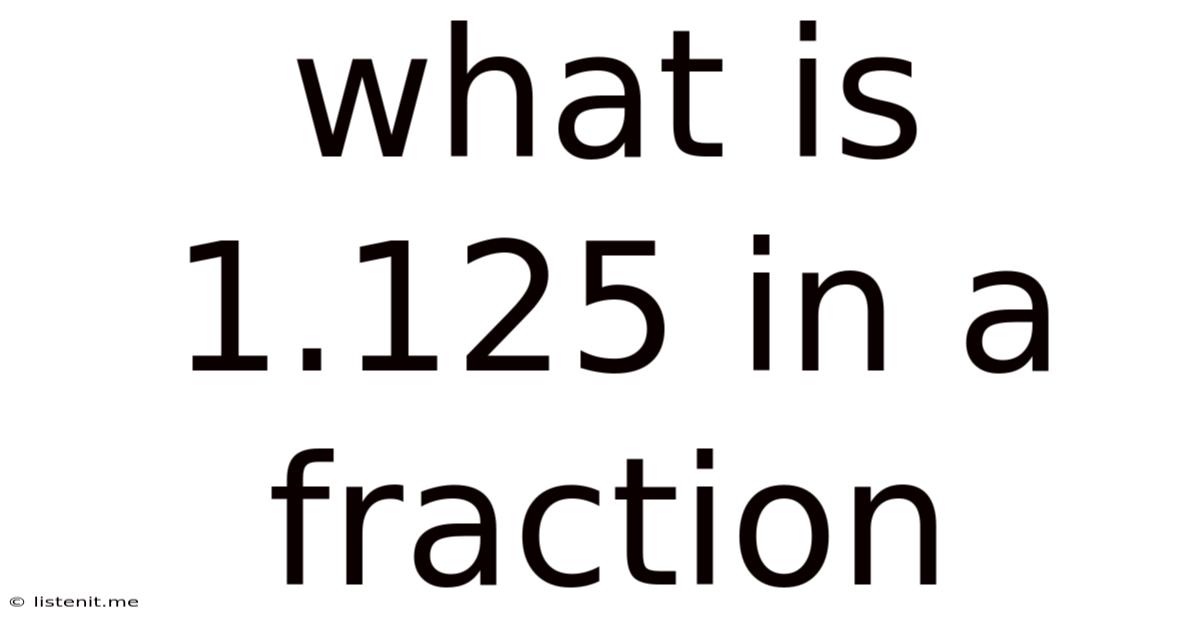
Table of Contents
What is 1.125 as a Fraction? A Comprehensive Guide
Converting decimals to fractions might seem daunting at first, but with a structured approach, it becomes a straightforward process. This comprehensive guide will walk you through the steps of converting 1.125 into a fraction, explaining the underlying principles and providing you with valuable techniques for tackling similar decimal-to-fraction conversions. We'll also explore related concepts and offer practical examples to solidify your understanding.
Understanding Decimals and Fractions
Before diving into the conversion, let's clarify the fundamental concepts of decimals and fractions.
-
Decimals: Decimals represent numbers that are not whole numbers. They use a decimal point to separate the whole number part from the fractional part. The digits after the decimal point represent tenths, hundredths, thousandths, and so on.
-
Fractions: Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many parts make up the whole.
The conversion process involves transforming the decimal representation (1.125) into its equivalent fractional representation (where the numerator and denominator are integers).
Converting 1.125 to a Fraction: Step-by-Step
Here's a step-by-step guide to convert 1.125 to a fraction:
Step 1: Identify the place value of the last digit.
In 1.125, the last digit (5) is in the thousandths place. This means the denominator of our fraction will be 1000.
Step 2: Write the decimal as a fraction with a denominator of 1000.
The decimal 1.125 can be written as:
1125/1000
Step 3: Simplify the fraction.
To simplify the fraction, we need to find the greatest common divisor (GCD) of the numerator (1125) and the denominator (1000). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Finding the GCD can be done using several methods, including:
- Prime factorization: Breaking down both numbers into their prime factors and identifying common factors.
- Euclidean algorithm: A more efficient method for larger numbers.
Let's use prime factorization for 1125 and 1000:
- 1125 = 3² x 5³
- 1000 = 2³ x 5³
The common factor is 5³. Therefore, the GCD is 125 (5 x 5 x 5 = 125).
Step 4: Divide both the numerator and the denominator by the GCD.
Dividing both the numerator and denominator by 125, we get:
(1125 ÷ 125) / (1000 ÷ 125) = 9/8
Step 5: Convert the improper fraction to a mixed number (optional).
The fraction 9/8 is an improper fraction (the numerator is larger than the denominator). We can convert it into a mixed number:
9/8 = 1 1/8
Therefore, 1.125 as a fraction is 9/8 or 1 1/8.
Alternative Methods for Decimal to Fraction Conversion
While the above method is the most common and generally preferred for decimals with a finite number of digits, there are other approaches you can employ:
Method 1: Using the Positional Value Directly
You can directly interpret the decimal places. 1.125 has a whole number part (1) and a fractional part (0.125). The fractional part is 125 thousandths, written as 125/1000. Then combine the whole number and the fraction: 1 + 125/1000 = 1 125/1000. Simplifying as before yields 1 1/8. This method is particularly helpful for understanding the underlying concept.
Method 2: Multiplying by a Power of 10
This method is especially useful when dealing with repeating decimals. However, for 1.125, it’s less efficient than the primary method outlined above. You would multiply by 1000 to remove the decimal point, getting 1125/1000, then simplify.
Practical Applications and Examples
Converting decimals to fractions is a skill with various applications in:
- Mathematics: Solving equations, simplifying expressions, and working with ratios and proportions.
- Science: Representing measurements, performing calculations involving fractions, and analyzing data.
- Engineering: Designing structures, calculating dimensions, and working with blueprints.
- Cooking and Baking: Following recipes accurately, adjusting ingredient quantities, and understanding ratios.
Example 1: Convert 0.375 to a fraction.
- The last digit (5) is in the thousandths place, so the denominator is 1000.
- The fraction is 375/1000.
- The GCD of 375 and 1000 is 125.
- Simplifying, we get 3/8.
Example 2: Convert 2.6 to a fraction.
- The last digit (6) is in the tenths place, so the denominator is 10.
- The fraction is 26/10.
- The GCD of 26 and 10 is 2.
- Simplifying, we get 13/5, which is equal to the mixed number 2 3/5.
Example 3: Convert 0.11111... (a repeating decimal) to a fraction. (Note: This is a more advanced case requiring different techniques than those used above for finite decimals)
Troubleshooting Common Mistakes
- Incorrectly Identifying the Place Value: Double-check the place value of the last digit to determine the correct denominator.
- Failing to Simplify Completely: Always simplify the fraction to its lowest terms. Using prime factorization or the Euclidean algorithm ensures complete simplification.
- Errors in GCD Calculation: Accurate calculation of the GCD is crucial. Use a calculator or practice finding the GCD to avoid errors.
- Improper Handling of Mixed Numbers: If you have an improper fraction, correctly convert it to a mixed number.
Conclusion
Converting decimals like 1.125 to fractions involves a systematic process of identifying the place value, writing the decimal as a fraction, finding the greatest common divisor, and simplifying the fraction. Understanding this process empowers you to confidently tackle various decimal-to-fraction conversions, expanding your mathematical skills and problem-solving capabilities across diverse applications. Remember to practice regularly to build fluency and accuracy in your conversions. The more you practice, the more intuitive this process will become.
Latest Posts
Latest Posts
-
Upper Pole Of Kidney On Ultrasound
Jun 05, 2025
-
Giant Cell Tumor Of Bone Histology
Jun 05, 2025
-
Basal Cell Chicken Pox Scar Leg
Jun 05, 2025
-
Lip Lowering Surgery For Gummy Smile
Jun 05, 2025
-
Cpt Code For In Vitro Fertilization
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 1.125 In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.