What Is 0.595 As A Fraction
listenit
May 25, 2025 · 5 min read
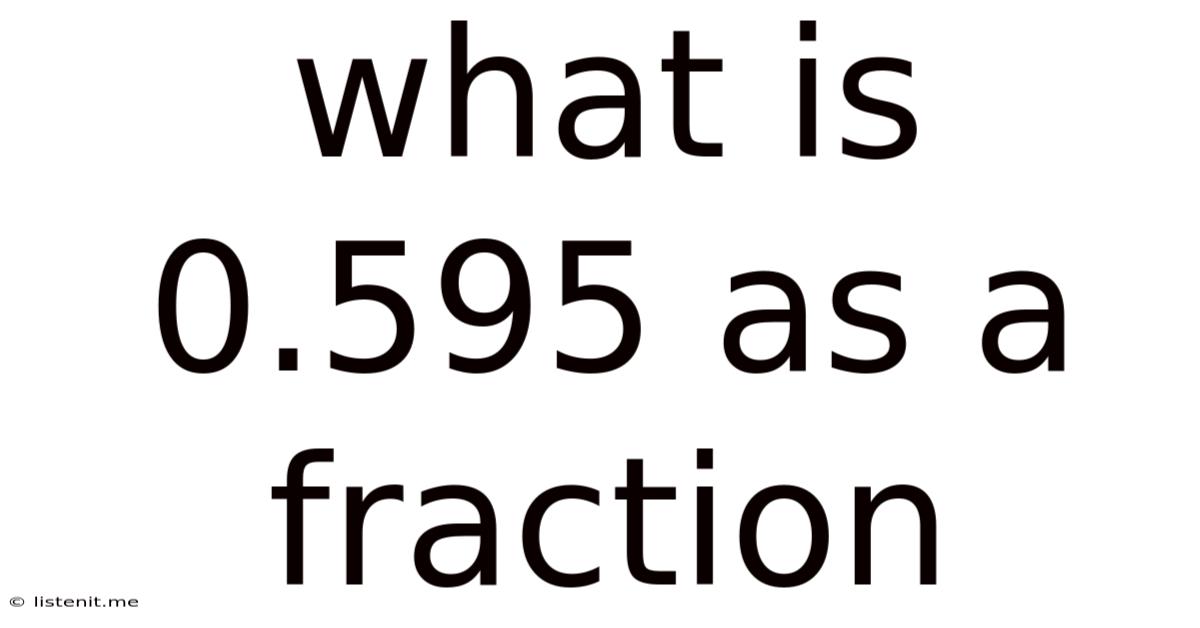
Table of Contents
What is 0.595 as a Fraction? A Comprehensive Guide
Converting decimals to fractions might seem daunting at first, but with a systematic approach, it becomes a straightforward process. This comprehensive guide will walk you through converting the decimal 0.595 into a fraction, explaining the steps in detail and providing additional context to enhance your understanding of decimal-to-fraction conversions. We'll cover various methods, address common misconceptions, and even explore related mathematical concepts.
Understanding Decimals and Fractions
Before we dive into the conversion, let's briefly revisit the fundamental concepts of decimals and fractions.
Decimals: Decimals represent fractional parts of a whole number using a base-ten system. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For example, in the decimal 0.595, the 5 to the right of the decimal point represents 5 tenths (5/10), the 9 represents 9 hundredths (9/100), and the final 5 represents 5 thousandths (5/1000).
Fractions: Fractions represent parts of a whole using a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts make up the whole. For example, 1/2 represents one part out of two equal parts.
Converting 0.595 to a Fraction: Step-by-Step
The key to converting a decimal to a fraction lies in understanding the place value of the last digit. In 0.595, the last digit (5) is in the thousandths place. This means the decimal can be written as 595/1000.
Step 1: Write the decimal as a fraction with a denominator of a power of 10.
0.595 can be written as 595/1000. This is because the decimal has three digits after the decimal point, which corresponds to the thousandths place (10<sup>3</sup> = 1000).
Step 2: Simplify the fraction (reduce to lowest terms).
The fraction 595/1000 is not in its simplest form. To simplify, we need to find the greatest common divisor (GCD) of the numerator (595) and the denominator (1000). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Finding the GCD can be done through various methods, including:
- Prime Factorization: Breaking down both numbers into their prime factors and identifying common factors.
- Euclidean Algorithm: A more efficient method for larger numbers.
Let's use prime factorization:
- 595 = 5 x 7 x 17
- 1000 = 2 x 2 x 2 x 5 x 5 x 5 = 2<sup>3</sup> x 5<sup>3</sup>
The only common factor is 5. Therefore, we divide both the numerator and the denominator by 5:
595 ÷ 5 = 119 1000 ÷ 5 = 200
This gives us the simplified fraction: 119/200
Therefore, 0.595 as a fraction is 119/200. This fraction is in its simplest form because 119 and 200 share no common factors other than 1.
Alternative Methods for Decimal to Fraction Conversion
While the above method is the most straightforward for decimals with a finite number of digits, there are alternative approaches:
Method 2: Using the place value directly
You can break down the decimal into its constituent parts based on place value and then add the fractions:
0.595 = 0.5 + 0.09 + 0.005 = 5/10 + 9/100 + 5/1000
To add these fractions, find a common denominator (1000 in this case):
= 500/1000 + 90/1000 + 5/1000 = 595/1000
Then, simplify as shown in the previous method to get 119/200.
Method 3: For Repeating Decimals
This method is particularly useful when dealing with repeating decimals (e.g., 0.333...). It involves setting up an equation and solving for the fraction. However, 0.595 is a terminating decimal, so this method is not necessary here.
Practical Applications and Real-World Examples
Understanding decimal-to-fraction conversions is crucial in various fields:
- Cooking and Baking: Recipes often use fractions for precise ingredient measurements. Converting decimal measurements to fractions ensures accuracy.
- Engineering and Construction: Precise calculations are essential in these fields. Converting decimals to fractions can help in maintaining accuracy and simplifying calculations.
- Finance: Dealing with percentages and proportions often involves converting decimals to fractions for clearer representation and easier calculations.
- Science: In scientific experiments and data analysis, fractions can sometimes offer a more intuitive representation of data than decimals.
Common Mistakes to Avoid
- Forgetting to simplify: Always simplify your fraction to its lowest terms. Leaving a fraction unsimplified can lead to errors in further calculations.
- Incorrectly identifying the place value: Make sure you correctly identify the place value of the last digit in the decimal. This is crucial for writing the correct initial fraction.
- Using incorrect simplification methods: Use a reliable method (prime factorization or Euclidean algorithm) to ensure accurate simplification.
Expanding Your Knowledge: Further Exploration of Fractions and Decimals
This guide provided a detailed explanation of converting 0.595 to a fraction. To further enhance your understanding, explore these related concepts:
- Converting fractions to decimals: Learn how to convert fractions to decimals, which is the reverse process of what we discussed.
- Operations with fractions and decimals: Practice adding, subtracting, multiplying, and dividing fractions and decimals.
- Working with mixed numbers: Understand how to convert mixed numbers (a whole number and a fraction) to improper fractions and vice-versa.
- Percentages and their relationship to fractions and decimals: Explore how percentages are closely related to fractions and decimals and how to convert between them.
By mastering decimal-to-fraction conversions, you'll enhance your mathematical skills and improve your ability to solve problems in various contexts. Remember to practice regularly and use different methods to strengthen your understanding. The more you practice, the more comfortable and confident you’ll become in handling these conversions. The conversion of 0.595 to 119/200 is a fundamental step in broader mathematical understanding.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 18 And 6
May 25, 2025
-
Chance Of Getting Pregnant By Age Calculator
May 25, 2025
-
Greatest Common Factor Of 60 And 90
May 25, 2025
-
30 Days Before October 31 2024
May 25, 2025
-
What Is 21 As A Fraction
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 0.595 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.