What Is 0.05 In A Fraction
listenit
Apr 03, 2025 · 5 min read
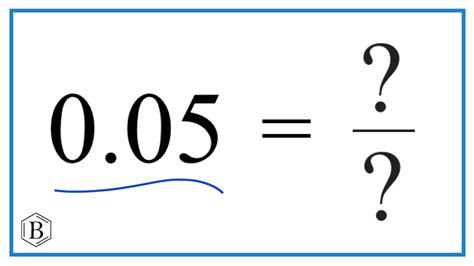
Table of Contents
What is 0.05 as a Fraction? A Comprehensive Guide
Decimal numbers are a common part of our daily lives, showing up in everything from financial transactions to scientific measurements. Understanding how to convert decimals to fractions is a crucial skill, and this guide will comprehensively explore the conversion of 0.05 into its fractional equivalent. We'll not only show you how to do it but also why the method works, ensuring a complete understanding of the underlying principles. This will cover various methods and delve into related concepts, making it suitable for various levels of mathematical understanding.
Understanding Decimal Places and Place Value
Before diving into the conversion, let's quickly review the concept of place value in decimals. The decimal point separates the whole number part from the fractional part. Each position to the right of the decimal point represents a power of ten in the denominator:
- 0.1: One-tenth (1/10)
- 0.01: One-hundredth (1/100)
- 0.001: One-thousandth (1/1000)
- And so on...
The number 0.05 has a '5' in the hundredths place. This means it represents five hundredths.
Method 1: Directly Writing the Fraction from the Decimal
The simplest method for converting 0.05 to a fraction directly leverages the place value understanding. Since the '5' is in the hundredths place, we can write it as:
5/100
This fraction represents five hundredths, directly reflecting the decimal value.
Method 2: Simplifying the Fraction
The fraction 5/100 is not in its simplest form. To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator (5) and the denominator (100) and divide both by it. The GCD of 5 and 100 is 5. Dividing both the numerator and the denominator by 5 gives us:
(5 ÷ 5) / (100 ÷ 5) = 1/20
Therefore, the simplest form of the fraction representing 0.05 is 1/20.
Method 3: Using the Power of Ten Method
This method involves writing the decimal as a fraction with a power of 10 as the denominator. Then, we simplify the fraction.
-
Write as a fraction over a power of 10: 0.05 can be written as 5/100 (since there are two digits after the decimal point, we use 10<sup>2</sup> or 100 as the denominator).
-
Simplify the fraction: As we've already done in Method 2, we simplify 5/100 to 1/20.
Method 4: Understanding the Relationship Between Decimals and Fractions
Decimals and fractions both represent parts of a whole. The key is to understand that the decimal system is based on powers of 10, while fractions represent parts of a whole using a numerator and a denominator. The conversion process involves expressing the decimal value as a ratio (fraction) that maintains its numerical equivalence.
Why These Methods Work: Mathematical Principles
The methods described above all rely on fundamental mathematical principles:
-
Place Value: The positional value of digits in a decimal number is crucial. Understanding place value allows us to directly translate the decimal into a fraction.
-
Equivalence of Fractions: Simplifying a fraction doesn't change its value; it simply expresses it in a more concise form. This principle ensures that 5/100 and 1/20 represent the same numerical quantity.
-
Greatest Common Divisor (GCD): Finding the GCD helps us find the largest number that divides both the numerator and denominator without leaving a remainder. This step is essential for simplifying fractions to their lowest terms.
Practical Applications of Converting Decimals to Fractions
The ability to convert decimals to fractions has numerous practical applications:
-
Cooking and Baking: Many recipes use fractions for ingredient measurements. Being able to convert decimal measurements (e.g., from a digital scale) to fractions is essential for accurate cooking.
-
Construction and Engineering: Precision is crucial in these fields. Converting decimals to fractions allows for more accurate calculations and measurements.
-
Finance: Understanding fractions is essential for comprehending interest rates, loan calculations, and other financial transactions.
-
Science and Mathematics: In scientific and mathematical calculations, fractions often provide a more precise representation of values than decimals.
Beyond 0.05: Converting Other Decimals to Fractions
The principles discussed here apply to converting any decimal to a fraction. The steps are generally the same:
-
Identify the place value of the last digit. This determines the denominator of the fraction.
-
Write the decimal as a fraction with a power of 10 as the denominator.
-
Simplify the fraction by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Example: Converting 0.25 to a fraction
-
The last digit (5) is in the hundredths place, so the denominator is 100.
-
Write the decimal as a fraction: 25/100
-
Simplify the fraction: 25/100 = 1/4 (GCD of 25 and 100 is 25).
Dealing with Repeating Decimals
Converting repeating decimals (like 0.333...) to fractions requires a slightly different approach, involving algebraic manipulation. This is a more advanced topic but essential for a comprehensive understanding of decimal-fraction conversion. A simple example involves setting up an equation, multiplying by a power of 10 to shift the decimal, and then solving for the unknown variable representing the fraction.
Conclusion: Mastering Decimal-to-Fraction Conversions
Converting decimals to fractions is a fundamental skill with widespread applications. By understanding place value, simplifying fractions, and applying the principles outlined in this guide, you can confidently convert any decimal number into its fractional equivalent. This understanding builds a solid foundation for more advanced mathematical concepts and problem-solving in various fields. Practice is key to mastering this skill, so try converting different decimals to fractions to solidify your understanding. Remember, the core principle remains consistent—expressing a decimal value as a ratio of two whole numbers.
Latest Posts
Latest Posts
-
Number Of Valence Electrons Of Potassium
Apr 04, 2025
-
The Most Abundant Gas In Our Atmosphere Is
Apr 04, 2025
-
How Does A Sedimentary Rock Turn Into A Metamorphic
Apr 04, 2025
-
Which Type Of Waves Are Sound Waves
Apr 04, 2025
-
Is Black Coffee A Homogeneous Mixture
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is 0.05 In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
