What Is 0.05 As A Percent
listenit
May 10, 2025 · 5 min read
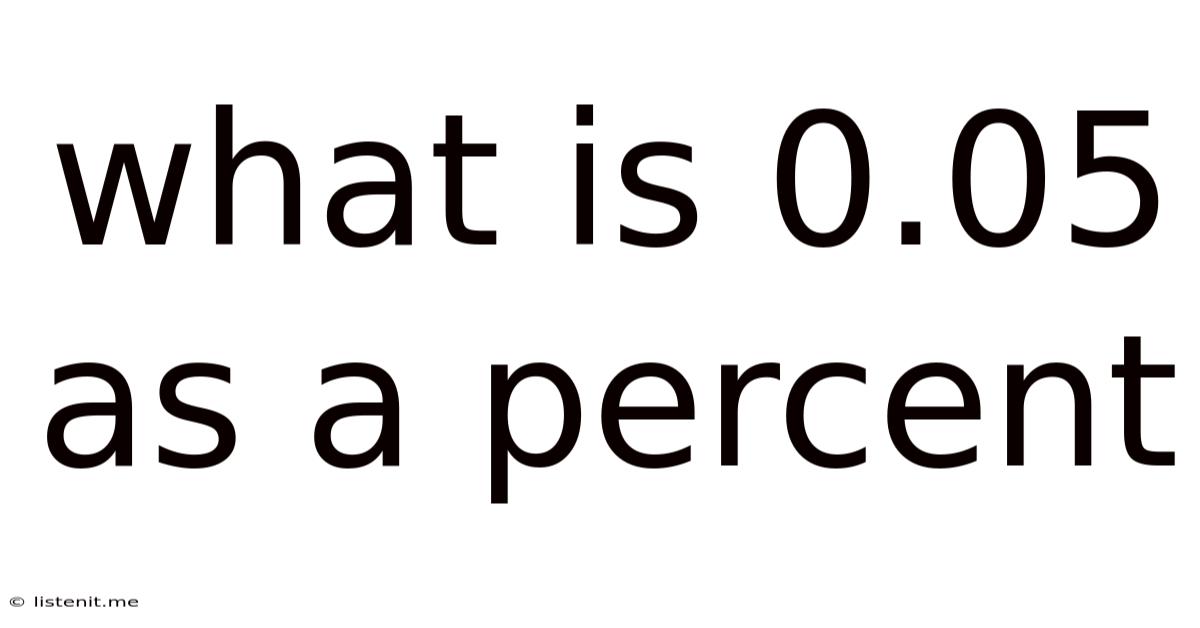
Table of Contents
What is 0.05 as a Percent? A Comprehensive Guide
Understanding decimal-to-percentage conversions is a fundamental skill in mathematics and across numerous fields. This comprehensive guide will delve into the conversion of 0.05 to a percentage, exploring the underlying principles and offering practical examples. We'll also touch upon the broader context of decimal-percentage conversions and their applications.
Understanding Decimals and Percentages
Before diving into the specific conversion of 0.05, let's refresh our understanding of decimals and percentages.
Decimals: Decimals represent fractional parts of a whole number. They use a base-ten system, with the digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on. For example, 0.05 represents five hundredths (5/100).
Percentages: Percentages express a proportion or fraction as a part of 100. The term "percent" literally means "per hundred" (Latin: per centum). A percentage is denoted by the symbol "%". For example, 5% means 5 out of 100, or 5/100.
Converting 0.05 to a Percentage
The conversion process from a decimal to a percentage involves multiplying the decimal by 100 and adding the percentage symbol. Here's how it's done for 0.05:
1. Multiply by 100:
0.05 x 100 = 5
2. Add the Percentage Symbol:
5 + % = 5%
Therefore, 0.05 as a percentage is 5%.
Practical Applications of 0.05 (5%)
Understanding the equivalence of 0.05 and 5% has numerous practical applications in various fields:
Finance and Investing:
- Interest Rates: A 5% interest rate on a savings account means you earn 5% of your principal balance annually.
- Investment Returns: An investment yielding 0.05 or 5% means it increased in value by 5% over a given period.
- Discount Rates: A 5% discount on a purchase means you pay 95% (100% - 5%) of the original price.
- Tax Rates: A 5% sales tax means that for every dollar spent, you pay an additional $0.05 (5 cents) in tax.
Science and Statistics:
- Probability: A probability of 0.05 (or 5%) indicates a 5% chance of an event occurring. This is frequently used in hypothesis testing where a p-value less than 0.05 suggests statistical significance.
- Data Analysis: Representing data as percentages provides a clearer and more intuitive understanding of proportions and trends compared to raw decimal values.
Everyday Life:
- Tip Calculation: A 5% tip on a restaurant bill represents 5% of the bill's total.
- Sales and Discounts: Retailers frequently advertise discounts as percentages (e.g., 5% off).
- Surveys and Polls: Results are usually presented as percentages to illustrate the proportion of respondents choosing a particular option.
Understanding the Concept of Percentage Change
In many real-world scenarios, we're often interested in calculating percentage change, which represents the relative change between two values. For example, if a stock price increases from $10 to $10.50, we can calculate the percentage change as follows:
- Find the difference: $10.50 - $10.00 = $0.50
- Divide by the original value: $0.50 / $10.00 = 0.05
- Multiply by 100 to express as a percentage: 0.05 x 100 = 5%
The stock price increased by 5%.
Converting Percentages to Decimals: The Reverse Operation
The reverse operation – converting a percentage to a decimal – is equally important. To do this, divide the percentage by 100. For example, to convert 5% back to a decimal:
5% / 100 = 0.05
This demonstrates the reversible nature of the conversion.
Advanced Applications: Compound Interest
Understanding percentages is crucial in calculating compound interest. Compound interest involves earning interest not only on the principal amount but also on the accumulated interest from previous periods. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Let's say you invest $1,000 at an annual interest rate of 5% (0.05), compounded annually (n=1), for 2 years (t=2):
A = 1000 (1 + 0.05/1)^(1*2) = $1102.50
After two years, your investment will be worth $1102.50, reflecting the effect of compound interest. Understanding the decimal equivalent (0.05) of the percentage (5%) is essential to applying this formula correctly.
Common Mistakes to Avoid When Working with Percentages
Several common errors can occur when working with percentages:
- Confusing decimals and percentages: Remember to multiply by 100 when converting decimals to percentages and divide by 100 when converting percentages to decimals.
- Incorrectly calculating percentage change: Always divide the difference by the original value when calculating percentage change.
- Mixing percentages with different bases: Ensure all percentages relate to the same base value when performing calculations involving multiple percentages.
- Rounding errors: Be mindful of rounding errors, especially when dealing with multiple calculations. Avoid rounding intermediate results prematurely.
Conclusion: Mastering Percentage Conversions
The conversion of 0.05 to 5% is a fundamental concept with widespread applications in various fields. Understanding this conversion, along with the broader principles of decimal-to-percentage conversions and the ability to perform related calculations, empowers you to handle various numerical tasks effectively. Whether it's calculating interest, analyzing data, or understanding discounts, the ability to confidently work with percentages is a valuable skill. Remember to practice these concepts regularly to reinforce your understanding and minimize potential errors. By mastering percentage conversions, you'll gain a significant advantage in many academic and professional settings.
Latest Posts
Latest Posts
-
Reaction Of Ammonium Chloride And Water
May 10, 2025
-
To Conduct Electricity A Solution Must Contain
May 10, 2025
-
How To Calculate The Image Distance
May 10, 2025
-
Examples Of Cacophony In A Sentence
May 10, 2025
-
Half Of 3 1 2 Inches
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 0.05 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.