What Are The Factors Of X2-100
listenit
May 13, 2025 · 5 min read
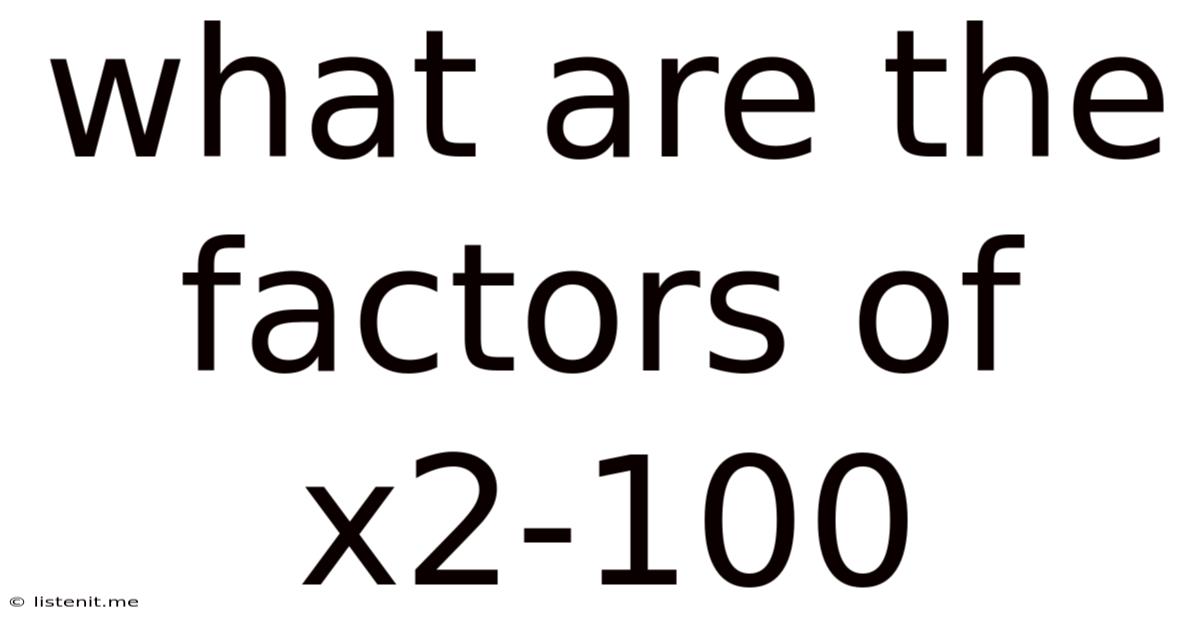
Table of Contents
What are the Factors of x² - 100? A Comprehensive Guide
Factoring quadratic expressions is a fundamental skill in algebra. Understanding how to factor these expressions unlocks the ability to solve quadratic equations, simplify complex algebraic expressions, and delve deeper into various mathematical concepts. This article will explore the factors of x² - 100 in detail, explaining the process, providing alternative methods, and showcasing its applications in various mathematical contexts.
Understanding the Problem: Factoring x² - 100
The expression x² - 100 represents a difference of squares. A difference of squares is a binomial (a polynomial with two terms) in the form a² - b², where 'a' and 'b' are any numbers or variables. In our case, a = x and b = 10 (since 10² = 100). The key to factoring a difference of squares lies in recognizing this specific pattern.
The Difference of Squares Formula
The general formula for factoring a difference of squares is:
a² - b² = (a + b)(a - b)
This formula states that the difference of two squares can always be factored into two binomials: one is the sum of the square roots and the other is the difference of the square roots.
Applying the Formula to x² - 100
Let's apply this formula to our expression, x² - 100:
-
Identify 'a' and 'b': We have a² = x², so a = x. We have b² = 100, so b = 10.
-
Substitute into the formula: Using the formula a² - b² = (a + b)(a - b), we substitute a = x and b = 10:
x² - 100 = (x + 10)(x - 10)
Therefore, the factors of x² - 100 are (x + 10) and (x - 10).
Verifying the Factors
We can verify our factorization by expanding the factored form:
(x + 10)(x - 10) = x(x - 10) + 10(x - 10) = x² - 10x + 10x - 100 = x² - 100
This confirms that our factorization is correct. The middle terms, -10x and +10x, cancel each other out, leaving us with the original expression.
Alternative Methods for Factoring
While the difference of squares formula is the most efficient method for this specific problem, let's explore alternative approaches that can be helpful for factoring other quadratic expressions:
1. Factoring by Grouping
Factoring by grouping is a technique used for factoring polynomials with four or more terms. While not directly applicable to x² - 100 (which has only two terms), it's a valuable method to know for other quadratic expressions.
2. Quadratic Formula
The quadratic formula is a powerful tool for finding the roots (solutions) of any quadratic equation in the form ax² + bx + c = 0. Once you find the roots, you can use them to factor the quadratic expression. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
For x² - 100, a = 1, b = 0, and c = -100. Substituting these values into the quadratic formula gives:
x = [0 ± √(0² - 4 * 1 * -100)] / 2 * 1 = ±√400 / 2 = ±20 / 2 = ±10
The roots are x = 10 and x = -10. Therefore, the factors are (x - 10) and (x + 10), which matches our previous result.
3. Completing the Square
Completing the square is another method for solving quadratic equations and can also be used to factor quadratic expressions. However, it's generally less efficient than the difference of squares formula for expressions like x² - 100.
Applications of Factoring x² - 100
The ability to factor x² - 100 has several practical applications in various areas of mathematics and beyond:
1. Solving Quadratic Equations
Factoring allows us to solve quadratic equations easily. If we have the equation x² - 100 = 0, we can factor it into (x + 10)(x - 10) = 0. This gives us two solutions: x = -10 and x = 10.
2. Simplifying Algebraic Expressions
Factoring can simplify more complex algebraic expressions. For example, consider the expression:
(x² - 100) / (x - 10)
By factoring the numerator, we get:
[(x + 10)(x - 10)] / (x - 10)
We can cancel out the (x - 10) terms, simplifying the expression to (x + 10), provided x ≠ 10.
3. Graphing Quadratic Functions
Understanding the factors of a quadratic expression helps in graphing the corresponding quadratic function. The factors represent the x-intercepts (where the graph crosses the x-axis). For the function y = x² - 100, the x-intercepts are -10 and 10. This information, along with the parabola's vertex and direction, helps create an accurate graph.
4. Calculus Applications
In calculus, factoring plays a crucial role in finding derivatives and integrals, particularly when dealing with polynomial functions. The ability to factor efficiently simplifies these calculations significantly.
5. Real-world Applications
Quadratic equations and their solutions find practical applications in various real-world scenarios, including physics (projectile motion), engineering (structural design), and economics (modeling supply and demand). The ability to factor quadratic expressions is therefore essential for solving problems in these fields.
Beyond x² - 100: Expanding Your Factoring Skills
While this article focused on factoring x² - 100, the principles and techniques discussed are applicable to a wide range of quadratic expressions and beyond. Practice is key to mastering factoring. Try factoring various quadratic expressions, experimenting with different methods, and gradually increasing the complexity of the problems. The more you practice, the more comfortable and proficient you'll become in this essential algebraic skill.
Conclusion: Mastering the Fundamentals of Factoring
The ability to factor quadratic expressions like x² - 100 is a cornerstone of algebraic proficiency. This article provided a thorough explanation of the process, explored alternative methods, and showcased the various applications of factoring in mathematics and beyond. By understanding and mastering this fundamental concept, you'll be well-equipped to tackle more complex mathematical challenges and succeed in various academic and professional fields. Remember, consistent practice is the key to unlocking your full potential in algebra and beyond!
Latest Posts
Latest Posts
-
Why Do Electric Field Lines Never Cross
May 13, 2025
-
1 10 As A Percent And Decimal
May 13, 2025
-
Can All Minerals Be A Gemstone
May 13, 2025
-
Multicellular Heterotrophs Without A Cell Wall
May 13, 2025
-
What Are The Gcf Of 48
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Are The Factors Of X2-100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.