What Are The Common Factors Of 6 And 12
listenit
Mar 29, 2025 · 5 min read
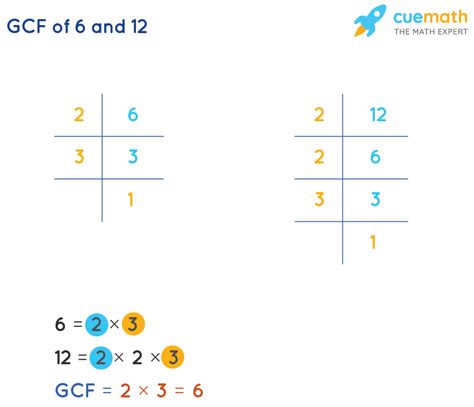
Table of Contents
What are the Common Factors of 6 and 12? A Deep Dive into Number Theory
Finding the common factors of two numbers might seem like a simple task, especially for small numbers like 6 and 12. However, understanding the underlying concepts reveals a fascinating glimpse into number theory, a branch of mathematics dealing with the properties of numbers. This exploration goes beyond simply stating the answer; we'll delve into the methods, definitions, and broader implications of finding common factors, illustrating the concepts with numerous examples and real-world applications.
Understanding Factors
Before diving into the common factors of 6 and 12, let's solidify our understanding of what a factor is. A factor (or divisor) of a number is a whole number that divides the number evenly, leaving no remainder. For instance:
- Factors of 6: 1, 2, 3, and 6 (because 6 ÷ 1 = 6, 6 ÷ 2 = 3, 6 ÷ 3 = 2, and 6 ÷ 6 = 1).
- Factors of 12: 1, 2, 3, 4, 6, and 12 (because 12 ÷ 1 = 12, 12 ÷ 2 = 6, 12 ÷ 3 = 4, 12 ÷ 4 = 3, 12 ÷ 6 = 2, and 12 ÷ 12 = 1).
Notice that both lists include 1 and the number itself. This is true for all numbers; 1 and the number itself are always factors.
Identifying Common Factors
Now, let's identify the common factors of 6 and 12. These are the numbers that appear in both lists of factors. Comparing the factors of 6 and 12, we see:
- Factors of 6: 1, 2, 3, 6
- Factors of 12: 1, 2, 3, 4, 6, 12
The numbers 1, 2, 3, and 6 appear in both lists. Therefore, the common factors of 6 and 12 are 1, 2, 3, and 6.
Greatest Common Factor (GCF)
Among the common factors, the greatest common factor (GCF), also known as the highest common factor (HCF), is the largest number that divides both numbers without leaving a remainder. In our example, the GCF of 6 and 12 is 6.
Methods for Finding the GCF
Several methods exist for finding the GCF, including:
-
Listing Factors: This method, which we used above, involves listing all the factors of each number and then identifying the largest common factor. This is effective for smaller numbers but becomes cumbersome for larger ones.
-
Prime Factorization: This method involves breaking down each number into its prime factors (factors that are only divisible by 1 and themselves). The GCF is the product of the common prime factors raised to the lowest power.
Let's illustrate this with 6 and 12:
- Prime factorization of 6: 2 x 3
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, the GCF is 2 x 3 = 6.
-
Euclidean Algorithm: This efficient algorithm is particularly useful for larger numbers. It repeatedly applies the division algorithm until the remainder is 0. The last non-zero remainder is the GCF. We won't delve into the details here, but it's a powerful technique for finding GCFs efficiently.
Applications of Common Factors and GCF
The concepts of common factors and the greatest common factor have numerous applications in various fields:
Mathematics:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 12/6 can be simplified to 2/1 (or simply 2) by dividing both the numerator and denominator by their GCF, which is 6.
-
Solving Equations: GCF plays a role in solving certain types of algebraic equations and in simplifying expressions.
-
Modular Arithmetic: Understanding factors is fundamental in modular arithmetic, a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus).
Real-World Applications:
-
Measurement and Division: Imagine you have 12 apples and 6 oranges, and you want to divide them into identical bags, with the same number of apples and oranges in each bag. The GCF (6) tells you that you can create 6 bags, each containing 2 apples and 1 orange.
-
Construction and Design: Common factors are relevant in designing structures or patterns where elements need to be arranged in uniform rows or columns. For example, arranging tiles or bricks.
-
Music and Rhythm: Musical rhythms and patterns often rely on common factors and multiples to create harmonious and repetitive sequences.
Extending the Concept: Least Common Multiple (LCM)
Closely related to the GCF is the least common multiple (LCM). The LCM of two numbers is the smallest number that is a multiple of both numbers. For 6 and 12:
- Multiples of 6: 6, 12, 18, 24, 30...
- Multiples of 12: 12, 24, 36, 48...
The smallest number that appears in both lists is 12. Therefore, the LCM of 6 and 12 is 12.
Relationship between GCF and LCM
There's a fascinating relationship between the GCF and LCM of two numbers:
(Number 1) x (Number 2) = GCF x LCM
Let's verify this for 6 and 12:
6 x 12 = 72 GCF(6, 12) x LCM(6, 12) = 6 x 12 = 72
This relationship holds true for any two numbers and provides a convenient method for finding the LCM if you already know the GCF (or vice versa).
Conclusion: Beyond the Basics
Finding the common factors of 6 and 12 might seem like a trivial exercise, but it opens a door to a rich world of mathematical concepts. Understanding factors, the GCF, and the LCM provides a foundational understanding of number theory, with applications that extend far beyond simple arithmetic. From simplifying fractions to solving complex equations and even designing rhythmic patterns, the principles explored here are fundamental to many aspects of mathematics and its real-world applications. This exploration encourages a deeper appreciation for the elegance and practicality of seemingly basic mathematical concepts. Further exploration into prime numbers, modular arithmetic, and other areas of number theory will only strengthen this foundation and reveal even more fascinating relationships within the world of numbers.
Latest Posts
Latest Posts
-
1 1 2 As An Improper Fraction
Apr 01, 2025
-
How To Find The X Intercepts Of A Parabola
Apr 01, 2025
-
What Is 1 9 As A Decimal
Apr 01, 2025
-
What Is The Inverse Of 3 X
Apr 01, 2025
-
Write 2 5 As A Decimal
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Are The Common Factors Of 6 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
