Use The Gcf To Factor 26+39
listenit
May 11, 2025 · 5 min read
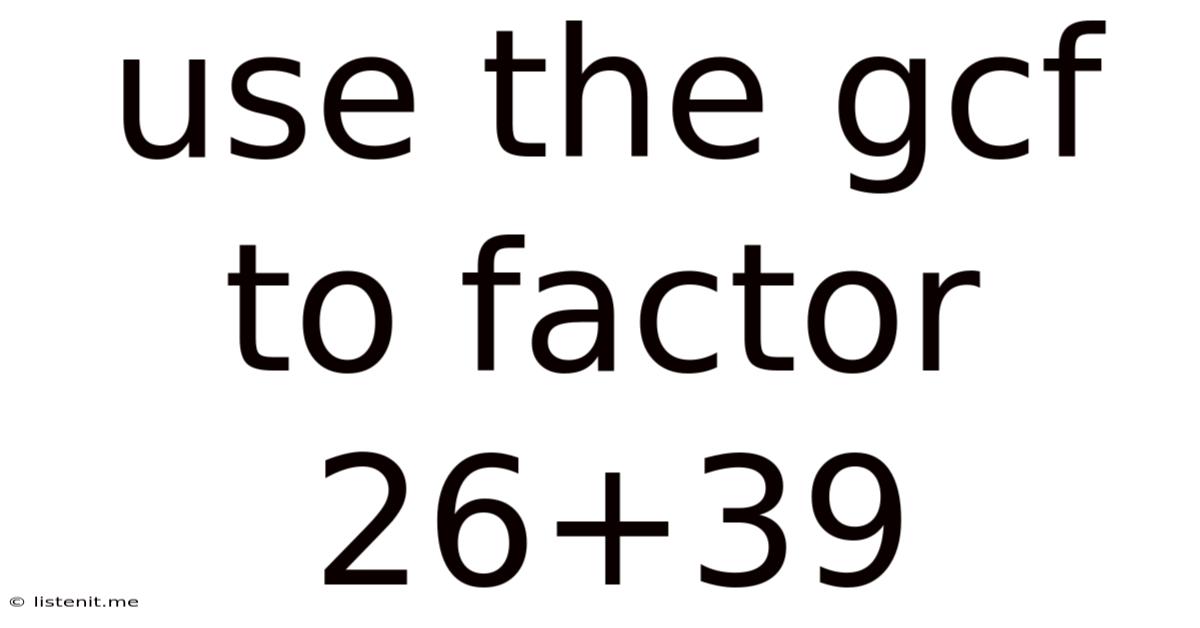
Table of Contents
Using the GCF to Factor 26 + 39: A Comprehensive Guide
Finding the greatest common factor (GCF) is a fundamental skill in algebra, crucial for simplifying expressions and solving equations. This article delves deep into the process of factoring using the GCF, using the expression 26 + 39 as a practical example. We'll explore various methods for finding the GCF, demonstrate the factoring process step-by-step, and extend the concept to more complex scenarios. By the end, you'll possess a solid understanding of this essential algebraic technique.
Understanding the Greatest Common Factor (GCF)
Before diving into factoring, let's solidify our understanding of the GCF. The GCF of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. For example, the GCF of 12 and 18 is 6, because 6 is the largest number that divides both 12 and 18 perfectly.
Finding the GCF is vital in simplifying expressions and solving various mathematical problems. It allows us to reduce complexity and express mathematical relationships in their most concise and manageable form. This is especially true when dealing with algebraic expressions.
Methods for Finding the GCF
Several methods can be employed to determine the GCF of numbers:
1. Listing Factors: This method involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 26: 1, 2, 13, 26
- Factors of 39: 1, 3, 13, 39
Comparing the lists, we see that the largest common factor is 13.
2. Prime Factorization: This method involves breaking down each number into its prime factors. The GCF is then the product of the common prime factors raised to the lowest power.
- Prime factorization of 26: 2 x 13
- Prime factorization of 39: 3 x 13
The common prime factor is 13. Therefore, the GCF of 26 and 39 is 13.
3. Euclidean Algorithm: This method is particularly efficient for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF. While less intuitive for smaller numbers like 26 and 39, it's invaluable for larger ones.
Factoring 26 + 39 Using the GCF
Now that we've established the GCF of 26 and 39 is 13, let's use it to factor the expression 26 + 39. The process is straightforward:
-
Identify the GCF: As determined above, the GCF of 26 and 39 is 13.
-
Divide each term by the GCF:
- 26 ÷ 13 = 2
- 39 ÷ 13 = 3
-
Rewrite the expression: The factored expression is 13(2 + 3).
Therefore, the factored form of 26 + 39 is 13(2 + 3). This simplified expression is equivalent to the original expression, but it is presented in a more concise and often more useful form.
Expanding the Concept: Factoring Polynomials
The principle of factoring using the GCF extends seamlessly to polynomials. Polynomials are algebraic expressions consisting of variables and constants, combined using addition, subtraction, multiplication, and non-negative integer exponents. Let's examine how to apply the GCF method to polynomials.
Consider the polynomial 15x² + 25x. To factor this polynomial using the GCF:
-
Identify the GCF of the coefficients: The GCF of 15 and 25 is 5.
-
Identify the GCF of the variables: Both terms contain 'x', and the lowest power of 'x' is x¹.
-
Determine the overall GCF: The GCF of 15x² and 25x is 5x.
-
Divide each term by the GCF:
- 15x² ÷ 5x = 3x
- 25x ÷ 5x = 5
-
Rewrite the polynomial: The factored polynomial is 5x(3x + 5).
Thus, the factored form of 15x² + 25x is 5x(3x + 5).
More Complex Examples and Applications
Let's explore more complex examples to further solidify our understanding.
Example 1: Factor 42a³b² + 21ab³
-
Find the GCF of coefficients: GCF(42, 21) = 21
-
Find the GCF of variables: GCF(a³, a) = a; GCF(b², b³) = b²
-
Overall GCF: 21a²b²
-
Factor: 21ab²(2a + b)
Example 2: Factor 18x³y²z + 27x²yz² + 9xyz³
-
GCF of coefficients: GCF(18, 27, 9) = 9
-
GCF of variables: GCF(x³, x², x) = x; GCF(y², y, y) = y; GCF(z, z², z³) = z
-
Overall GCF: 9xyz
-
Factor: 9xyz(2x²y + 3xz + z²)
These examples demonstrate the versatility of the GCF method in factoring various types of polynomials, regardless of their complexity. The key is to systematically identify the greatest common factor among all the terms and then factor it out.
Real-World Applications of Factoring
Factoring, particularly using the GCF, is not merely an abstract mathematical exercise. It has practical applications in various fields:
-
Physics and Engineering: Factoring simplifies equations used to model physical phenomena, making them easier to analyze and solve.
-
Computer Science: Factoring is crucial in cryptography and algorithm optimization.
-
Economics and Finance: Factoring is used in mathematical models for financial analysis and forecasting.
-
Geometry and Calculus: Factoring simplifies geometric formulas and expressions encountered in calculus.
Conclusion: Mastering GCF Factoring
The ability to factor using the GCF is a foundational skill in algebra and beyond. Through the examples and explanations provided, you should now have a comprehensive understanding of how to find the GCF and utilize it for effective factoring. This skill will serve as a crucial building block for tackling more advanced algebraic concepts and solving a wide range of mathematical problems across various disciplines. Remember to practice regularly; the more you practice, the more proficient you'll become at quickly and accurately identifying the GCF and factoring expressions. This skill is an invaluable tool in your mathematical arsenal.
Latest Posts
Latest Posts
-
Why Did Communism Appeal To Poor People In Russia
May 11, 2025
-
Find The Area Enclosed By The Figure
May 11, 2025
-
What Is 0 465 Converted To A Percentage
May 11, 2025
-
What Made Vietnam War So Difficult
May 11, 2025
-
Why Is Dna Replication A Semi Conservative Process
May 11, 2025
Related Post
Thank you for visiting our website which covers about Use The Gcf To Factor 26+39 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.