Two Lines Perpendicular To The Same Plane Are
listenit
Mar 28, 2025 · 4 min read
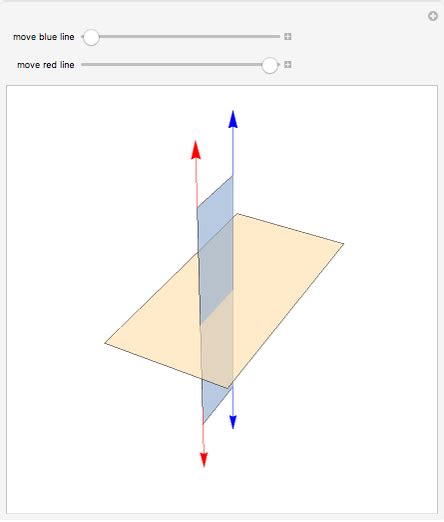
Table of Contents
Two Lines Perpendicular to the Same Plane Are… Parallel?
Understanding spatial relationships between lines and planes is fundamental in geometry. A common question that arises is: what is the relationship between two lines that are both perpendicular to the same plane? The short answer is that they are parallel. This article will delve deep into this concept, providing a rigorous proof and exploring its implications in various applications.
Defining the Terms
Before we dive into the proof, let's clearly define the terms involved:
-
Plane: A flat, two-dimensional surface that extends infinitely in all directions. We can represent a plane using a linear equation in three dimensions (e.g., Ax + By + Cz + D = 0).
-
Line: A one-dimensional object extending infinitely in both directions. A line in three-dimensional space can be described using parametric equations or vector equations.
-
Perpendicular: Two lines are perpendicular if the angle between them is 90 degrees. A line is perpendicular to a plane if it is perpendicular to every line in the plane that intersects it. This is equivalent to saying the line is perpendicular to any two non-parallel lines within the plane.
Proving the Parallelism
We will use a vector approach to prove that two lines perpendicular to the same plane are parallel. This method offers a concise and elegant demonstration.
Theorem: If two lines are perpendicular to the same plane, then the two lines are parallel.
Proof:
Let's consider plane P and two lines, l1 and l2, both perpendicular to plane P. Let's represent the direction vectors of these lines as v1 and v2, respectively. Since l1 is perpendicular to plane P, its direction vector v1 is normal (perpendicular) to plane P. Similarly, since l2 is perpendicular to plane P, its direction vector v2 is also normal to plane P.
Now, consider the set of all vectors normal to plane P. These vectors are all scalar multiples of each other. This is because if a vector is normal to a plane, any scalar multiple of that vector will also be normal to the plane. Therefore, there exists a scalar k such that:
v2 = kv1
This equation implies that v1 and v2 are linearly dependent. Two vectors are parallel if and only if they are linearly dependent. Since v1 and v2 are the direction vectors of lines l1 and l2, respectively, and they are linearly dependent, the lines l1 and l2 must be parallel. This completes the proof.
Visualizing the Concept
Imagine a flat tabletop (representing the plane). Now, imagine two perfectly upright pencils standing on the table. Both pencils are perpendicular to the tabletop. Visually, it's clear that the pencils are parallel to each other. This simple analogy effectively illustrates the theorem.
Implications and Applications
The theorem that two lines perpendicular to the same plane are parallel has numerous practical implications across various fields:
1. Engineering and Construction:
In structural engineering and building construction, understanding the parallelism of lines perpendicular to a plane is crucial for ensuring stability and structural integrity. For instance, in designing a building's framework, the columns (lines perpendicular to the ground plane) need to be parallel to maintain structural balance and prevent collapse.
2. Computer Graphics and 3D Modeling:
In computer graphics and 3D modeling, this concept is fundamental in defining the orientation and positioning of objects in three-dimensional space. Creating parallel lines perpendicular to a plane is essential for generating accurate and realistic 3D models.
3. Navigation and Mapping:
In navigation and mapping systems, understanding the relationship between lines and planes is vital for accurate calculations of distance, direction, and positioning. Determining parallel lines perpendicular to a reference plane aids in navigation tasks.
4. Physics and Mechanics:
In physics and mechanics, this concept is used in various applications involving forces and vectors. For instance, understanding the parallelism of forces acting perpendicular to a surface is critical in analyzing the equilibrium of a system.
Advanced Concepts and Extensions
The fundamental concept of parallelism between lines perpendicular to the same plane extends to more complex geometrical scenarios:
-
Skew Lines: While lines perpendicular to the same plane are parallel, it's important to distinguish this from skew lines. Skew lines are lines that do not intersect and are not parallel; they lie in different planes.
-
Higher Dimensions: This concept can be extended to higher dimensions. In n-dimensional space, lines perpendicular to the same (n-1)-dimensional hyperplane will also be parallel.
-
Applications in Linear Algebra: The proof using vectors highlights the strong connection between this geometrical theorem and concepts in linear algebra, such as linear dependence and vector spaces.
Conclusion
The seemingly simple statement – two lines perpendicular to the same plane are parallel – underpins many significant concepts in geometry and its applications. Through a clear understanding of the definitions, a rigorous proof, and an exploration of its implications, we've established the validity and importance of this fundamental geometrical principle. This knowledge is invaluable across numerous fields, from engineering and construction to computer graphics and physics, highlighting the interconnectedness of mathematical concepts and their real-world applications. The power of this simple theorem lies not only in its elegance but also in its wide-ranging applicability in solving complex problems across diverse domains.
Latest Posts
Latest Posts
-
How Do You Find Change In Velocity
Mar 31, 2025
-
What Percent Is 5 Out Of 8
Mar 31, 2025
-
Is H2s An Acid Or Base
Mar 31, 2025
-
What Is 83333 As A Fraction
Mar 31, 2025
-
Least Common Multiple 16 And 24
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Two Lines Perpendicular To The Same Plane Are . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
