The Difference Of 12 And 20 Of A Number X
listenit
May 12, 2025 · 5 min read
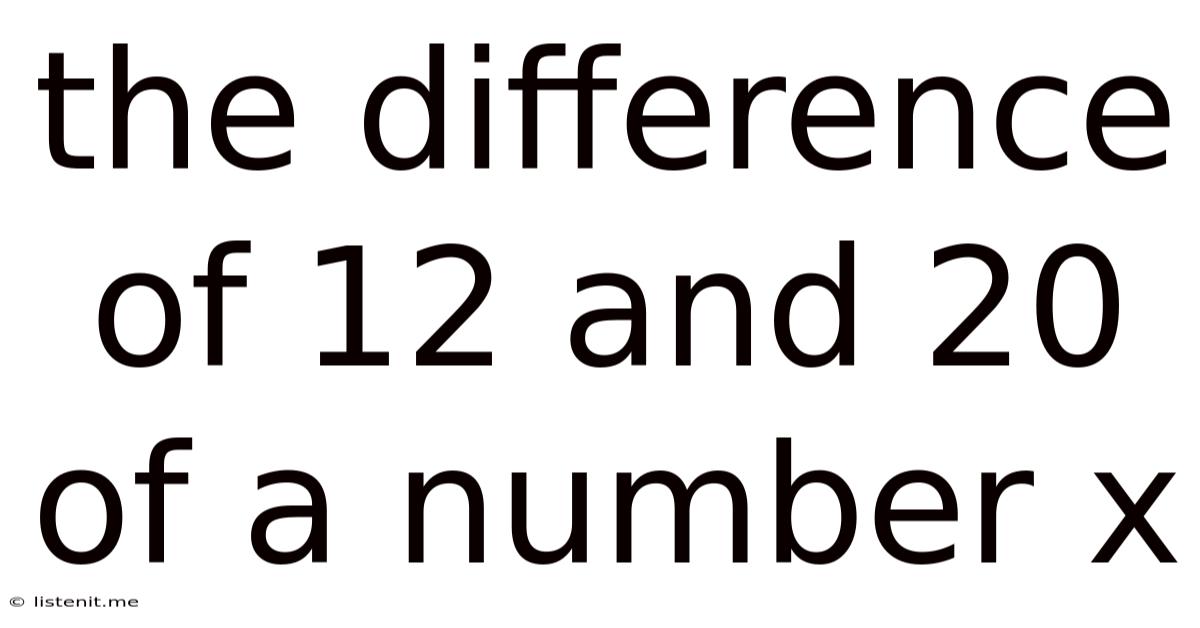
Table of Contents
Unveiling the Mysteries: Exploring the Differences Between 12x and 20x
Mathematics, at its core, is about understanding relationships and patterns. One fundamental aspect of this involves exploring the differences between multiples of a number. This article delves into the fascinating world of comparing 12 times a number (12x) and 20 times that same number (20x), uncovering the nuances of their difference and exploring its implications across various mathematical contexts. We'll unpack the core mathematical principles, illustrate with real-world examples, and highlight the practical applications of understanding this relationship.
The Fundamental Difference: 8x
The most straightforward way to understand the difference between 12x and 20x is to simply subtract one from the other:
20x - 12x = 8x
This simple equation reveals the fundamental truth: the difference between 20 times a number and 12 times that same number is always 8 times the number itself (8x). This remains consistent regardless of the value of 'x'. Whether x is a positive integer, a negative number, a fraction, or even an irrational number like π, the difference will always be a multiple of 8.
Visualizing the Difference
Imagine you have 'x' number of apples. If you have 20 times that amount (20x apples), and you give away 12 times the original amount (12x apples), you'll be left with 8 times the original amount (8x apples). This simple analogy effectively illustrates the core concept.
Exploring Different Values of 'x'
Let's explore how the difference (8x) behaves with different types of 'x':
1. Positive Integers:
If x = 5, then 20x = 100 and 12x = 60. The difference is 100 - 60 = 40, which is indeed 8 * 5 = 40.
If x = 100, then 20x = 2000 and 12x = 1200. The difference is 2000 - 1200 = 800, again confirming that 8 * 100 = 800.
This demonstrates that the difference remains consistent across various positive integer values of 'x'.
2. Negative Numbers:
If x = -3, then 20x = -60 and 12x = -36. The difference is -60 - (-36) = -24. Note that 8 * (-3) = -24, further solidifying the relationship. The difference remains consistent even with negative numbers.
3. Fractions and Decimals:
If x = 0.5, then 20x = 10 and 12x = 6. The difference is 10 - 6 = 4. This aligns perfectly with 8 * 0.5 = 4.
If x = 2/3, then 20x = 40/3 and 12x = 24/3. The difference is (40/3) - (24/3) = 16/3. This also aligns with 8 * (2/3) = 16/3.
This demonstrates the consistency of the relationship irrespective of the nature of 'x'.
4. Irrational Numbers:
Even with irrational numbers, the relationship holds. If x = π (approximately 3.14159), then the difference between 20π and 12π will be approximately 8π, which is about 25.1327. The underlying principle remains unaffected by the nature of 'x'.
Real-World Applications and Examples
The concept of the difference between 12x and 20x isn't merely an academic exercise; it finds practical applications in various real-world scenarios:
1. Profit Calculation:
Imagine a business sells a product for $20 per unit (20x, where x is the number of units sold). Their production cost is $12 per unit (12x). Their profit per unit is the difference: $20 - $12 = $8 (8x). By understanding this relationship, they can easily calculate their total profit based on the number of units sold.
2. Financial Investments:
Suppose you invest in two different schemes. Scheme A yields a return of 20% of your investment (20x, where x is the initial investment), while scheme B yields 12%. The difference in returns is 8% of your investment (8x), providing a clear comparison between the two investment options.
3. Comparative Analysis:
In many scenarios comparing two values, the difference between 12x and 20x can be crucial. For instance, if two companies' market share is represented as 12x% and 20x%, the difference (8x%) directly reflects the competitive edge of the company with the larger market share.
4. Resource Allocation:
Consider a project requiring 20 units of a resource (20x, where x is a unit of resource). If only 12 units are currently available (12x), the shortfall is 8 units (8x), highlighting the need for additional resource allocation.
Expanding the Concept: Generalizing the Difference Between 'ax' and 'bx'
The relationship between 12x and 20x can be generalized to understand the difference between any two multiples of a number 'x'. If we have 'ax' and 'bx', where 'a' and 'b' are constants, the difference is always (a - b)x. This formula provides a powerful tool to analyze the difference between any two multiples of a given quantity.
For instance, if we want to find the difference between 35x and 17x, it's simply (35 - 17)x = 18x. This formula streamlines comparisons across diverse mathematical problems.
Conclusion: The Power of Understanding Multiplicative Relationships
Understanding the difference between 12x and 20x, and its generalization to 'ax' and 'bx', opens doors to a deeper comprehension of multiplicative relationships in mathematics. This knowledge is far from theoretical; it provides a practical framework for solving various real-world problems, from calculating profits and analyzing investments to assessing resource needs and comparing competitive standings. The seemingly simple equation, 20x - 12x = 8x, represents a powerful tool for anyone looking to analyze quantitative data and make informed decisions. By mastering this fundamental concept, you enhance your mathematical prowess and your ability to solve complex problems with greater ease and efficiency. It's a testament to the power of simple mathematical relationships in illuminating complex scenarios.
Latest Posts
Related Post
Thank you for visiting our website which covers about The Difference Of 12 And 20 Of A Number X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.