Sum Of Interior Angles Of Hexagon
listenit
Apr 07, 2025 · 6 min read
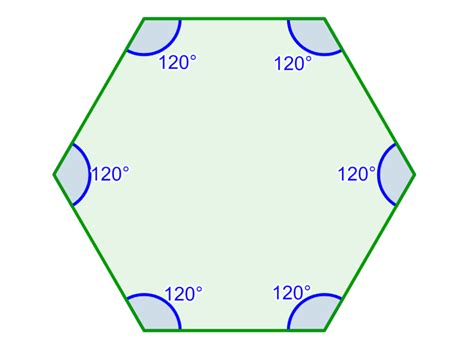
Table of Contents
The Sum of Interior Angles of a Hexagon: A Comprehensive Guide
The sum of the interior angles of a polygon, a closed two-dimensional shape with straight sides, is a fundamental concept in geometry. Understanding this concept is crucial for various applications, from architecture and engineering to computer graphics and game development. This article delves deep into the sum of interior angles of a hexagon, exploring different methods of calculation, providing real-world examples, and examining related geometrical principles.
What is a Hexagon?
Before we delve into the sum of interior angles, let's establish a firm understanding of what a hexagon is. A hexagon is a polygon with six sides and six angles. Hexagons come in various forms, including:
- Regular Hexagon: All sides and angles are equal. Each interior angle measures 120 degrees.
- Irregular Hexagon: Sides and angles are of varying lengths and measures. The sum of its interior angles, however, remains consistent.
- Convex Hexagon: All interior angles are less than 180 degrees.
- Concave Hexagon: At least one interior angle is greater than 180 degrees.
Understanding these different types of hexagons is important because, while their shapes vary, the formula for calculating the sum of their interior angles remains the same.
Calculating the Sum of Interior Angles: The Formula
The most efficient way to calculate the sum of the interior angles of any polygon, including a hexagon, is using a general formula. This formula relates the number of sides of the polygon to the sum of its interior angles. The formula is:
Sum of Interior Angles = (n - 2) × 180°
Where 'n' represents the number of sides of the polygon.
For a hexagon, n = 6. Substituting this value into the formula, we get:
Sum of Interior Angles = (6 - 2) × 180° = 4 × 180° = 720°
Therefore, the sum of the interior angles of any hexagon, regardless of its shape (regular or irregular, convex or concave), is always 720 degrees.
Methods to Prove the Formula and the Sum for a Hexagon
While the formula provides a quick and easy way to calculate the sum of interior angles, understanding the underlying principles is equally important. Let's explore different methods to prove the formula and apply it to a hexagon:
1. Triangulation Method
This method involves dividing the hexagon into triangles. A hexagon can be divided into four triangles by drawing diagonals from one vertex to the other non-adjacent vertices. Each triangle has an interior angle sum of 180°. Since there are four triangles, the total sum of interior angles is 4 * 180° = 720°. This visually demonstrates why the (n-2) x 180° formula works.
2. Exterior Angle Approach
The sum of the exterior angles of any polygon is always 360°. If we consider one exterior angle at each vertex of the hexagon, the total sum of the exterior angles is 360°. Since each interior angle and its corresponding exterior angle are supplementary (they add up to 180°), we can find the sum of the interior angles. Let's denote the interior angles as I1, I2, I3, I4, I5, and I6, and the exterior angles as E1, E2, E3, E4, E5, and E6. We know that:
I1 + E1 = 180° I2 + E2 = 180° I3 + E3 = 180° I4 + E4 = 180° I5 + E5 = 180° I6 + E6 = 180°
Adding these equations, we get:
(I1 + I2 + I3 + I4 + I5 + I6) + (E1 + E2 + E3 + E4 + E5 + E6) = 6 * 180° = 1080°
Since the sum of exterior angles (E1 + E2 + E3 + E4 + E5 + E6) = 360°, we have:
Sum of Interior Angles (I1 + I2 + I3 + I4 + I5 + I6) = 1080° - 360° = 720°
3. Mathematical Induction (Advanced)
While more complex, mathematical induction provides a rigorous proof for the formula's validity for all polygons, including hexagons. This method involves proving a base case (e.g., a triangle) and then showing that if the formula holds for an n-sided polygon, it also holds for an (n+1)-sided polygon. This ensures the formula's consistency across all polygons.
Real-World Applications of Hexagons and Interior Angle Calculations
The concept of hexagons and their interior angles finds numerous applications in various fields:
-
Honeycomb Structure: Honeybees construct their honeycombs using hexagonal cells. The hexagonal shape maximizes space utilization and strength with minimal material. Understanding the interior angles is crucial for analyzing the structural integrity of the honeycomb.
-
Architecture and Engineering: Hexagonal designs are employed in various architectural structures and engineering projects. From floor tiling patterns to bridge designs, the inherent stability of hexagons makes them an attractive choice. Calculating interior angles helps ensure structural stability and load distribution.
-
Computer Graphics and Game Development: Hexagonal grids are used in game development to create maps and represent game spaces. Understanding interior angles is essential for accurate calculations of movement, collision detection, and pathfinding.
-
Crystallography: Many crystals exhibit hexagonal structures. Understanding the angles within these structures is vital for determining crystal properties and predicting their behavior.
-
Nature: Hexagonal patterns appear naturally in various phenomena, including snowflakes, basalt columns, and certain plant structures. The mathematical principles underlying these patterns are rooted in the properties of hexagons and their interior angles.
Solving Problems Involving Hexagons and Interior Angles
Let's consider a few examples illustrating the application of the sum of interior angles in hexagon-related problems:
Example 1:
A regular hexagon has an interior angle of 120°. Verify that the sum of its interior angles is 720°.
Solution: Since it's a regular hexagon, all six angles are equal to 120°. The sum is 6 * 120° = 720°. This confirms the general formula.
Example 2:
An irregular hexagon has five interior angles measuring 110°, 125°, 130°, 140°, and 150°. Find the measure of the sixth interior angle.
Solution: The sum of the interior angles of any hexagon is 720°. Let x be the measure of the sixth angle. Then:
110° + 125° + 130° + 140° + 150° + x = 720°
655° + x = 720°
x = 720° - 655° = 65°
Therefore, the sixth interior angle measures 65°.
Example 3:
A hexagon is divided into triangles. How many triangles are formed? What is the relationship between the number of triangles and the sum of the interior angles?
Solution: A hexagon can be divided into four triangles. The sum of the interior angles is 4 * 180° = 720°, demonstrating the direct relationship between the number of triangles and the total interior angle sum.
Conclusion
The sum of interior angles of a hexagon, consistently 720°, is a fundamental concept with far-reaching implications. Understanding this concept and the various methods for calculating it are essential for various fields. From the elegant structures of honeycombs to the complex designs in engineering and computer graphics, the hexagon's properties offer valuable insights into the world around us. By mastering the calculation of interior angles, we unlock a deeper understanding of geometry and its practical applications. Remember, whether you're dealing with a regular or irregular hexagon, the sum of its interior angles will always be 720°. This constant provides a reliable foundation for solving a wide range of geometrical problems.
Latest Posts
Latest Posts
-
Graph Of Absolute Value Of X 1
Apr 08, 2025
-
What Are The Steps Of The Dna Ladder Made Of
Apr 08, 2025
-
The True Power Is Dissipated By The Of Any Circuit
Apr 08, 2025
-
How Did Hoover Respond To The Bonus Army
Apr 08, 2025
-
Find An Equation Of The Perpendicular Bisector
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Sum Of Interior Angles Of Hexagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.