Square Root Of X 2 1
listenit
May 09, 2025 · 5 min read
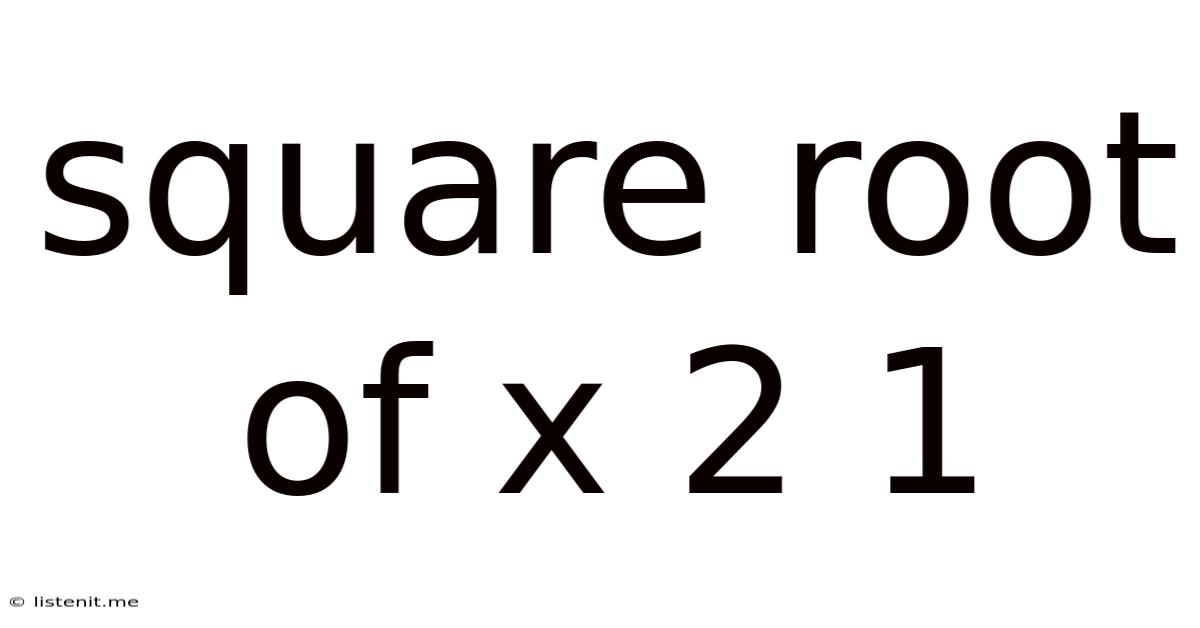
Table of Contents
Delving Deep into the Square Root of x² + 1: A Comprehensive Exploration
The expression √(x² + 1) appears frequently in various fields, from calculus and physics to computer graphics and engineering. Understanding its properties, behavior, and applications is crucial for anyone working with these areas. This article provides a comprehensive exploration of √(x² + 1), examining its mathematical properties, graphical representation, applications, and related concepts.
Mathematical Properties of √(x² + 1)
The square root of x² + 1 is a non-linear function, meaning its output doesn't change proportionally with its input. This seemingly simple expression holds several significant mathematical characteristics:
1. Domain and Range:
-
Domain: The domain of √(x² + 1) encompasses all real numbers, from negative infinity to positive infinity (-∞, ∞). This is because x² is always non-negative, meaning x² + 1 is always positive or zero, and the square root of a non-negative number is always defined in the real number system.
-
Range: The range of the function is [1, ∞). The minimum value occurs when x = 0, resulting in √(0² + 1) = 1. As x increases (positively or negatively), the value of √(x² + 1) also increases without bound.
2. Even Function:
√(x² + 1) is an even function. This means that f(-x) = f(x) for all x in the domain. In simpler terms, the function is symmetrical about the y-axis. This symmetry stems directly from the fact that (-x)² = x².
3. No Zeros:
The function √(x² + 1) has no zeros. This is because x² + 1 is always greater than or equal to 1, and the square root of a number greater than 1 is always greater than 1. Therefore, the function never intersects the x-axis.
4. Derivative and Integral:
Calculating the derivative and integral of √(x² + 1) provides further insights into its behavior:
-
Derivative: Using the chain rule, the derivative of √(x² + 1) is: x / √(x² + 1). This derivative is always defined for all real x.
-
Integral: The indefinite integral of √(x² + 1) is more complex and requires techniques like trigonometric substitution. The result involves a combination of hyperbolic functions and a logarithmic term, typically expressed as:
(1/2) * [x√(x² + 1) + ln|x + √(x² + 1)|] + C (where C is the constant of integration)
5. Relationship to Hyperbolic Functions:
The expression √(x² + 1) is closely related to hyperbolic functions, specifically the hyperbolic cosine (cosh x). Recall that cosh x = (eˣ + e⁻ˣ)/2. While not directly equivalent, the function's behavior shares similarities with hyperbolic cosine.
Graphical Representation of √(x² + 1)
Plotting the graph of y = √(x² + 1) reveals its key features:
-
Shape: The graph starts at the point (0, 1) and increases monotonically as x moves away from zero in either direction (positive or negative). The curve approaches a linear growth rate as |x| becomes large. The symmetry around the y-axis is clearly visible.
-
Asymptotic Behavior: While the function is not asymptotic in the traditional sense (it doesn't approach a horizontal asymptote), its growth rate resembles a linear function for large values of |x|. The curve gets increasingly steeper as x moves towards positive or negative infinity.
-
Concavity: The concavity of the graph changes. Initially, it's concave down, near (0,1) but gradually transitions towards a linear appearance where the curvature reduces.
Applications of √(x² + 1)
The expression √(x² + 1) finds applications across various disciplines:
1. Calculus and Analysis:
-
Arc Length: It appears in calculations of arc length for curves, particularly those defined parametrically.
-
Integration Problems: As mentioned earlier, it features prominently in integration problems requiring advanced techniques like trigonometric substitution.
-
Differential Equations: It appears in the solutions of certain types of differential equations.
2. Physics and Engineering:
-
Special Relativity: It's integral to calculations related to Lorentz transformations in special relativity, specifically when dealing with spacetime intervals.
-
Mechanics: It can emerge in problems involving the calculation of forces or velocities in certain mechanical systems.
-
Signal Processing: It might appear in Fourier transforms or other signal processing algorithms.
3. Computer Graphics and Game Development:
-
3D Transformations: It plays a role in various 3D transformations and rotations, particularly when dealing with normalized vectors.
-
Physics Engines: It’s used in calculations related to physics simulations, such as projectile motion or collision detection.
4. Statistics and Probability:
- Normal Distribution: While not a direct component, the function's characteristics are relevant to understanding the behavior of the normal distribution's tail probabilities.
Related Concepts and Extensions
Understanding √(x² + 1) is enhanced by exploring related concepts:
1. Hyperbolic Trigonometry:
As discussed, this function has a close relationship with hyperbolic trigonometric functions, providing alternative ways to analyze and represent it. Exploring hyperbolic functions deepens understanding of the expression’s behavior and properties.
2. Complex Numbers:
Expanding the domain to include complex numbers opens up further possibilities for analysis and application. The expression can be evaluated for complex values of x, leading to complex-valued results.
3. Approximations:
For large values of x, √(x² + 1) can be approximated by |x| (the absolute value of x). This approximation simplifies calculations when high accuracy is not critical. Understanding the error involved in this approximation is important.
Conclusion: A Versatile Mathematical Expression
The expression √(x² + 1), seemingly simple at first glance, reveals its depth and versatility through mathematical analysis and its broad applications across various fields. Understanding its mathematical properties, graphical representation, and the contexts in which it appears is crucial for anyone working with mathematics, physics, engineering, computer science, and related areas. Its connection to hyperbolic functions, its role in advanced calculus, and its presence in numerous applied settings underline its importance in both theoretical and practical contexts. Further exploration of its properties and applications will undoubtedly reveal even more of its significance.
Latest Posts
Latest Posts
-
Does The Following Molecule Have A Dipole Moment
May 10, 2025
-
Cos X In Terms Of Sin X
May 10, 2025
-
A Pure Substance That Cannot Be Broken Down
May 10, 2025
-
Change The Fraction 3 4 To A Percent
May 10, 2025
-
The Ultimate Source Of Energy In Food Is
May 10, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of X 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.