Square Root Of 2 Times 8
listenit
May 10, 2025 · 6 min read
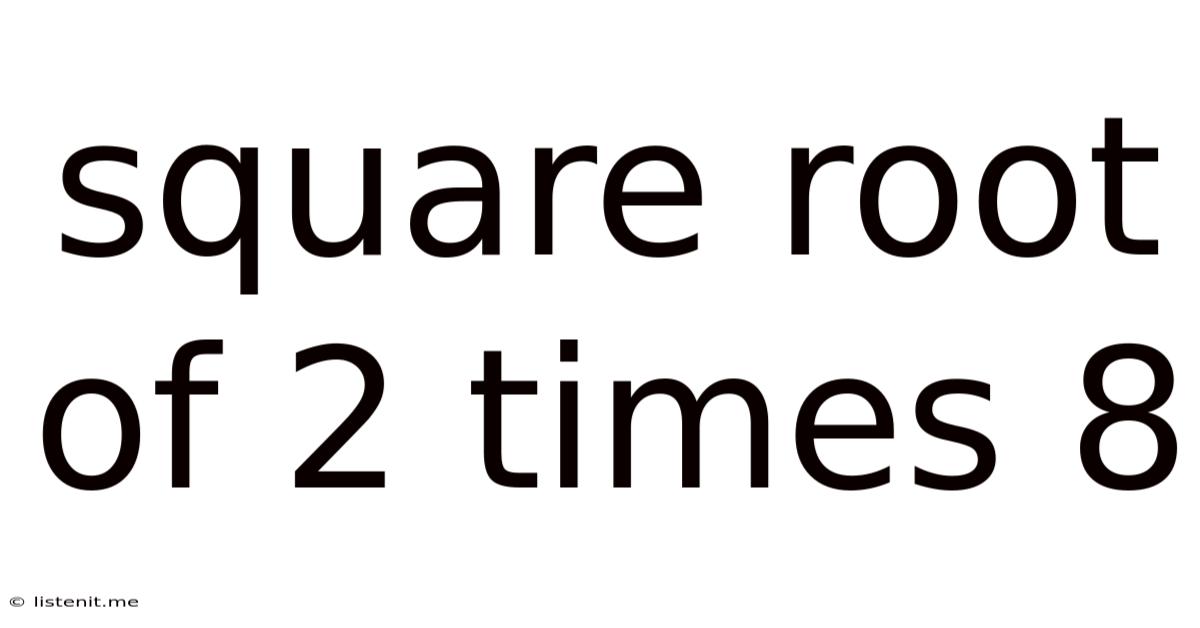
Table of Contents
Decoding the Mystery: A Deep Dive into √2 x 8
The seemingly simple expression √2 x 8 might appear innocuous at first glance. However, a closer examination reveals a fascinating interplay between irrational and rational numbers, offering a rich opportunity to explore fundamental mathematical concepts. This article delves deep into the calculation, its implications, and related mathematical principles, aiming to provide a comprehensive understanding suitable for both beginners and those seeking a deeper appreciation of mathematical elegance.
Understanding the Components: √2 and 8
Before tackling the multiplication, let's break down the individual components:
√2: The Irrational Number
√2, or the square root of 2, represents a number that, when multiplied by itself, equals 2. This number is irrational, meaning it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation is non-terminating and non-repeating: 1.41421356... This irrationality is a key characteristic that significantly impacts the overall result of our calculation. Understanding the nature of irrational numbers is crucial to grasping the complexities of mathematical operations involving them. The discovery of irrational numbers was a pivotal moment in the history of mathematics, challenging the Pythagorean belief that all numbers could be expressed as ratios of integers. The proof of the irrationality of √2 is a classic example of proof by contradiction, a powerful technique in mathematical reasoning.
8: The Rational Number
In contrast to √2, 8 is a rational number. It can be expressed as a simple fraction (8/1) and its decimal representation terminates (8.0). Rational numbers are far easier to work with than irrational numbers in many mathematical contexts due to their finite and easily manageable representations. The contrast between the rational 8 and the irrational √2 highlights the diverse types of numbers that exist within the mathematical system. This contrast becomes particularly important when considering the outcome of multiplying these two different types of numbers.
Calculating √2 x 8: A Step-by-Step Approach
Now, let's address the main task: calculating √2 x 8. The process is straightforward:
1. Commutative Property: Multiplication is commutative, meaning the order of the operands doesn't affect the result. Therefore, √2 x 8 is equivalent to 8 x √2.
2. Multiplication: We multiply the rational number 8 by the irrational number √2. This results in a new irrational number: 8√2. We cannot simplify this further by converting it into a rational number; it remains an irrational number.
3. Approximation: While 8√2 is the exact answer, we can obtain an approximate decimal value by using an approximation for √2. Using a calculator or a known approximation (such as 1.414), we can calculate:
8 x 1.414 ≈ 11.312
This is an approximation, not the exact value. The more decimal places we use for √2, the more accurate our approximation will be. The inherent nature of irrational numbers necessitates the use of approximations in many practical applications.
Exploring the Implications: Irrationality and its Consequences
The result, 8√2, underscores several important mathematical concepts:
-
Closure under Multiplication: The set of real numbers is closed under multiplication. This means that multiplying any two real numbers (rational or irrational) always results in another real number. In our case, the product of a rational number (8) and an irrational number (√2) yields another irrational number (8√2).
-
The Nature of Irrational Numbers: The result reinforces the concept that multiplying a rational number by an irrational number generally results in an irrational number (unless the rational number is zero). This is a significant characteristic that distinguishes irrational numbers from rational numbers.
-
Approximation and Error: The need for approximation highlights the limitations of representing irrational numbers in decimal form. Any decimal representation of 8√2 will necessarily be an approximation, carrying an inherent degree of error. The precision of this approximation depends on the number of decimal places used for √2. The concept of error and its propagation is crucial in various fields like engineering and scientific calculations.
Extending the Exploration: Related Mathematical Concepts
The simple calculation of √2 x 8 opens doors to exploring various related mathematical concepts:
1. Geometric Interpretation:
Consider a square with side length √2. Its area would be (√2)² = 2 square units. Now, imagine 8 such squares arranged together. The combined area would be 8 x 2 = 16 square units. This geometric interpretation provides a visual representation of the calculation.
2. Trigonometry and the Unit Circle:
√2 appears frequently in trigonometry, particularly when dealing with angles of 45 degrees. The coordinates of the point on the unit circle corresponding to a 45-degree angle involve √2. Understanding the relationship between √2 and trigonometry provides a deeper appreciation of its significance in mathematical contexts beyond simple multiplication.
3. Continued Fractions:
Irrational numbers like √2 can be represented as continued fractions—an infinite expression of nested fractions. Exploring the continued fraction representation of √2 provides a unique perspective on its inherent structure and allows for a different approach to calculating approximations.
4. Series Expansions:
√2 can also be expressed using infinite series expansions, such as Taylor series or other convergent series. These series offer yet another method for approximating the value of √2 and consequently, 8√2.
5. Number Theory:
The study of √2 touches upon various aspects of number theory, including the concept of quadratic irrationals and the properties of algebraic numbers. Exploring these areas provides insights into the deeper mathematical structure and properties of irrational numbers.
Practical Applications and Real-World Relevance
While seemingly abstract, the understanding of irrational numbers and calculations involving them holds significant practical value:
-
Engineering and Physics: Calculations in various engineering and physics disciplines frequently involve irrational numbers like √2. For example, in structural engineering, calculations related to diagonal lengths often involve √2.
-
Computer Graphics and Game Development: Rendering and calculations in computer graphics and game development make extensive use of mathematical concepts involving irrational numbers. Understanding and efficiently handling these calculations is essential for optimizing performance.
-
Financial Modeling: Financial models sometimes incorporate irrational numbers in their calculations, particularly when dealing with complex interest rates or stochastic processes.
-
Signal Processing: Signal processing algorithms often rely on mathematical operations involving irrational numbers in various aspects of signal analysis and manipulation.
Conclusion: A Deeper Appreciation of Mathematical Beauty
The seemingly simple calculation of √2 x 8 has led us on a journey through the fascinating world of irrational numbers, revealing their importance and the nuances of working with them. From the fundamental properties of rational and irrational numbers to the practical applications in various fields, this exploration has shed light on the richness and beauty of mathematics. Understanding the interplay between rational and irrational numbers is crucial for a comprehensive grasp of mathematical concepts and their applications in real-world scenarios. The seemingly simple expression serves as a microcosm of the broader mathematical landscape, reminding us of the endless depth and complexity waiting to be uncovered within seemingly simple equations. The journey of understanding √2 x 8 is not merely about arriving at a numerical answer; it is about appreciating the elegance and complexity of the mathematical structures that underpin our world.
Latest Posts
Latest Posts
-
Write The Polynomial As A Product Of Linear Factors
May 10, 2025
-
Is Melting Sugar A Chemical Or Physical Change
May 10, 2025
-
Speed Of Sound In Air Vs Water
May 10, 2025
-
7 5 4x 2 3x 8
May 10, 2025
-
What Is The Multiplicative Inverse Of 3
May 10, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 2 Times 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.