Square Root Of 1 Tan 2c
listenit
May 11, 2025 · 4 min read
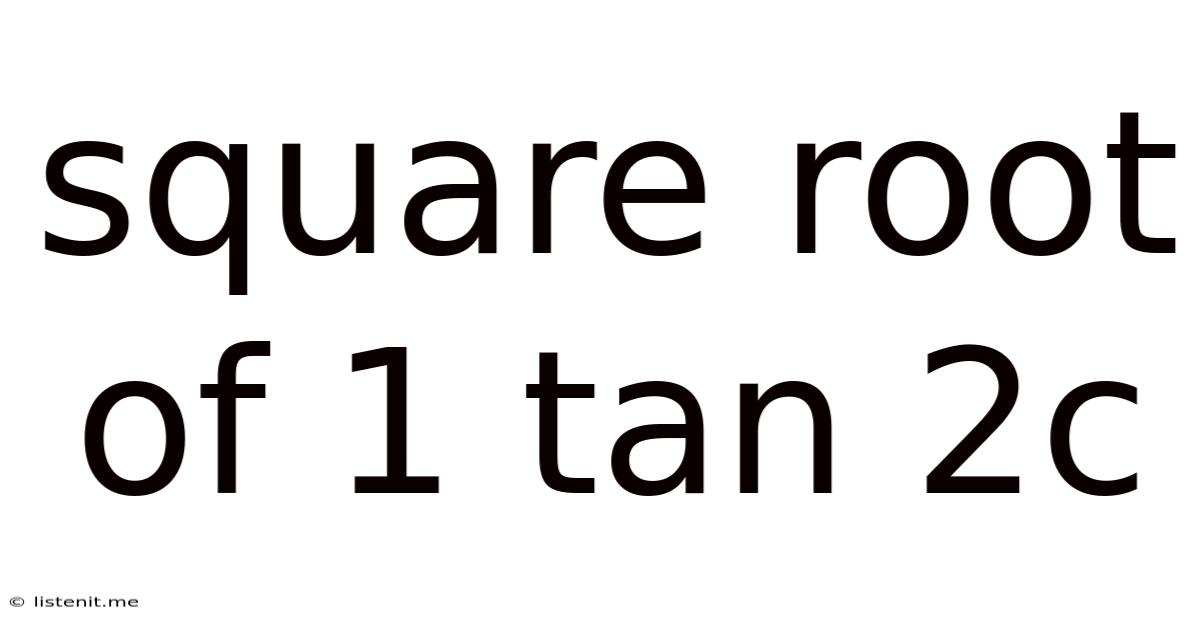
Table of Contents
Exploring the Square Root of 1 + Tan²c: A Deep Dive into Trigonometric Identities
The expression √(1 + tan²c) might seem deceptively simple at first glance. However, it represents a fundamental concept in trigonometry with far-reaching implications in various fields, from physics and engineering to computer graphics and beyond. This article delves deep into understanding this expression, exploring its derivation, applications, and its relationship to other trigonometric identities.
Understanding the Core Identity: Pythagorean Trigonometric Identities
The key to unlocking the meaning of √(1 + tan²c) lies in the Pythagorean trigonometric identities. These identities are foundational relationships between sine, cosine, and tangent functions, stemming directly from the Pythagorean theorem applied to a right-angled triangle. The most relevant identity for our exploration is:
sin²c + cos²c = 1
This identity is universally true for any angle 'c'. From this, we can derive other useful identities. Let's explore how.
Deriving the Identity Relevant to √(1 + tan²c)
Recall that the tangent function is defined as:
tan c = sin c / cos c
If we divide the fundamental Pythagorean identity (sin²c + cos²c = 1) by cos²c, we get:
(sin²c / cos²c) + (cos²c / cos²c) = 1 / cos²c
This simplifies to:
tan²c + 1 = sec²c
Therefore, we can rewrite our original expression as:
√(1 + tan²c) = √(sec²c)
This simplifies further, considering the definition of the secant function:
sec c = 1 / cos c
Therefore:
√(sec²c) = |sec c| = |1 / cos c|
The absolute value is crucial here. The square root of a squared value always results in a non-negative value, while the secant function itself can be negative depending on the quadrant in which the angle 'c' lies.
Interpreting the Result: Quadrantal Analysis
The expression |1/cos c| highlights the importance of considering the quadrant in which the angle 'c' resides. Let's break this down:
-
First Quadrant (0° < c < 90°): In this quadrant, both sine and cosine are positive, making the secant positive. Therefore, |1/cos c| = 1/cos c = sec c.
-
Second Quadrant (90° < c < 180°): Cosine is negative in this quadrant, making the secant negative. Thus, |1/cos c| = -1/cos c = -sec c.
-
Third Quadrant (180° < c < 270°): Both sine and cosine are negative, resulting in a positive secant. Therefore, |1/cos c| = 1/cos c = sec c.
-
Fourth Quadrant (270° < c < 360°): Cosine is positive, and the secant is positive. Therefore, |1/cos c| = 1/cos c = sec c.
Applications in Various Fields
The expression √(1 + tan²c) and its simplification to |sec c| have wide-ranging applications across diverse fields. Let's explore some examples:
1. Physics and Engineering:
In physics and engineering, trigonometric functions are frequently used to model oscillatory motion, wave phenomena, and vector analysis. The simplification of √(1 + tan²c) to |sec c| simplifies complex calculations involving angles and forces, especially in situations where the direction of a vector plays a crucial role. For example, calculating the magnitude of a resultant force that is decomposed into its horizontal and vertical components can utilize this identity.
2. Computer Graphics and Game Development:
In computer graphics and game development, trigonometric functions are essential for tasks such as 3D rotations, transformations, and rendering. Understanding the relationship between the tangent, secant, and angle greatly simplifies calculations related to camera positioning, object orientation, and lighting effects. The identity is crucial for efficient and accurate vector manipulation.
3. Navigation and Surveying:
Navigation and surveying rely heavily on trigonometric calculations to determine distances, angles, and positions. This identity is particularly useful in scenarios involving oblique triangles, where the simplification provided by this identity can streamline calculations of distances or heights based on angle measurements.
4. Electrical Engineering:
In electrical engineering, trigonometric functions are indispensable for analyzing alternating current (AC) circuits. Phasors, which represent AC signals as vectors, rely on trigonometric relationships. This identity can aid in calculating the impedance and phase relationships within AC circuits, leading to simplified calculations of current and voltage.
Advanced Applications and Extensions
Beyond the basic applications mentioned above, the identity √(1 + tan²c) = |sec c| serves as a building block for more complex trigonometric manipulations.
1. Calculus:
In calculus, the derivative and integral of trigonometric functions are frequently encountered. The identity provides a way to simplify expressions involving tangent and secant functions, making differentiation and integration simpler.
2. Complex Numbers:
The identity has connections with complex numbers and their representation in the complex plane. Through Euler's formula (e^(ix) = cos x + i sin x), the relationship between trigonometric functions and exponential functions is revealed, expanding the applicability of the identity to complex number analysis.
Conclusion: The Significance of a Simple Expression
While √(1 + tan²c) might appear to be a straightforward trigonometric expression, its simplification to |sec c| unlocks significant possibilities. Understanding this identity's derivation and implications is crucial for anyone working with trigonometry, whether in the realm of pure mathematics or applied fields such as physics, engineering, computer graphics, or navigation. Its widespread applicability and fundamental nature underscore its importance as a cornerstone of mathematical understanding. By mastering this identity, one gains a deeper appreciation of the elegance and power of trigonometric relationships, opening doors to more advanced mathematical concepts and practical applications. Moreover, understanding the nuances of quadrantal analysis ensures accuracy and precision in calculations involving this important identity.
Latest Posts
Latest Posts
-
How To Find Y Intercept With Slope And A Point
May 12, 2025
-
What Would Happen If The Earth Had No Tilt
May 12, 2025
-
How To Find The Area Under A Normal Distribution Curve
May 12, 2025
-
What Is 4 36 In Simplest Form
May 12, 2025
-
What Is The Decimal Of 9 10
May 12, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 1 Tan 2c . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.