Square Root Of -1 Over 8
listenit
May 09, 2025 · 5 min read
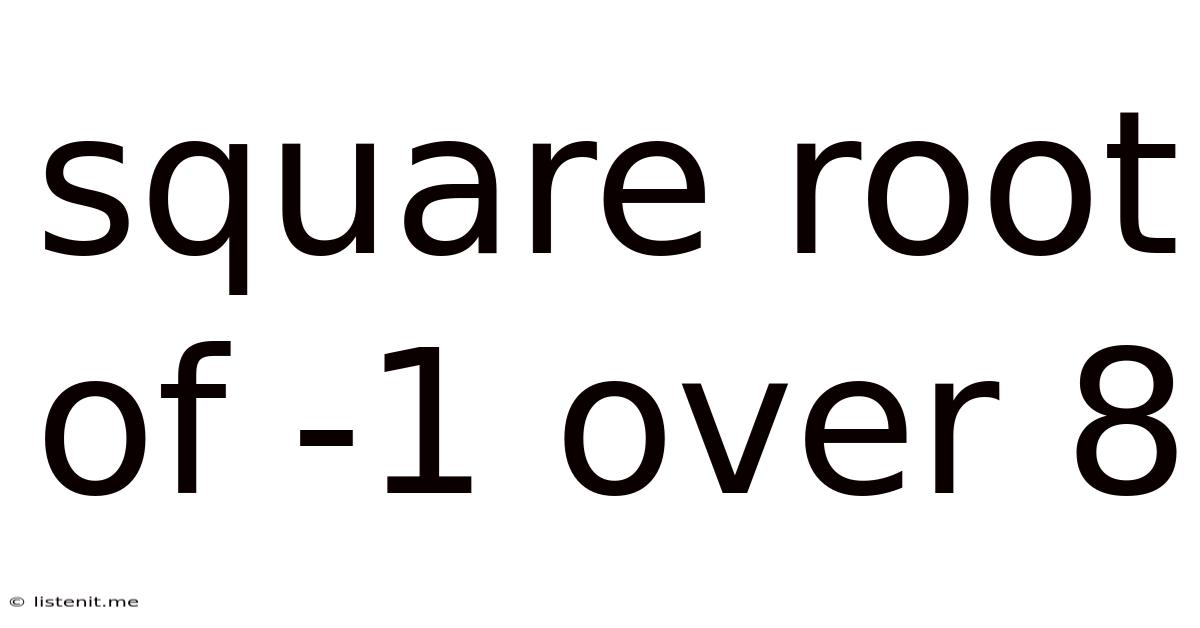
Table of Contents
Delving into the Depths: Exploring the Mathematical Enigma of √(-1)/8
The expression √(-1)/8, seemingly simple at first glance, opens a fascinating window into the world of complex numbers and their multifaceted applications across various scientific and engineering disciplines. This article delves deep into the mathematical underpinnings of this expression, exploring its properties, interpretations, and significance within the broader context of complex analysis.
Understanding the Fundamentals: Imaginary and Complex Numbers
Before embarking on a detailed analysis of √(-1)/8, it's crucial to establish a firm understanding of the fundamental building blocks: imaginary and complex numbers.
The Imaginary Unit, i:
The square root of -1, denoted as i, forms the cornerstone of imaginary numbers. This seemingly paradoxical concept arises from the inability to find a real number whose square is negative. Mathematicians introduced i to expand the number system and address equations that previously had no solutions within the realm of real numbers. i possesses the following key property:
i² = -1
This simple equation unlocks a whole new dimension of mathematical possibilities.
Complex Numbers: The Marriage of Real and Imaginary:
A complex number combines a real number and an imaginary number. It's typically expressed in the form:
z = a + bi
where:
- a is the real part (Re(z))
- b is the imaginary part (Im(z))
- i is the imaginary unit
Complex numbers greatly extend the capabilities of mathematics, enabling the solution of previously unsolvable equations and providing a richer framework for representing various physical phenomena.
Deconstructing √(-1)/8: A Step-by-Step Analysis
Now, let's dissect the expression √(-1)/8. We can break it down as follows:
-
The Square Root of -1: This component, as discussed earlier, is the imaginary unit i.
-
Division by 8: This simply scales the imaginary unit down by a factor of 8.
Therefore, √(-1)/8 can be elegantly expressed as:
√(-1)/8 = i/8 = 0 + (1/8)i
This representation clearly shows that √(-1)/8 is a complex number with a real part of 0 and an imaginary part of 1/8.
Visualizing Complex Numbers: The Complex Plane
Complex numbers can be effectively visualized using the complex plane (also known as the Argand plane). This two-dimensional plane has a horizontal axis representing the real part and a vertical axis representing the imaginary part. √(-1)/8, with its real part 0 and imaginary part 1/8, would be plotted as a point (0, 1/8) on the complex plane, lying on the positive imaginary axis.
Polar Form: An Alternative Representation
Besides the Cartesian form (a + bi), complex numbers can also be represented in polar form using magnitude (r) and argument (θ). The magnitude represents the distance of the point from the origin, while the argument is the angle the line connecting the origin and the point makes with the positive real axis.
For √(-1)/8:
- Magnitude (r): |i/8| = 1/8
- Argument (θ): π/2 radians (or 90 degrees) This is because the point lies on the positive imaginary axis.
Thus, the polar form of √(-1)/8 is:
(1/8)(cos(π/2) + i sin(π/2))
This representation provides a geometric interpretation of the complex number, highlighting its magnitude and direction on the complex plane. Euler's formula further simplifies this representation:
(1/8)e^(iπ/2)
Applications of Complex Numbers and √(-1)/8
The seemingly simple expression √(-1)/8 finds applications in diverse fields:
1. Electrical Engineering: AC Circuit Analysis
Complex numbers are essential tools in analyzing alternating current (AC) circuits. Impedance, a measure of opposition to the flow of current, is often represented as a complex number, encompassing both resistance and reactance (due to inductors and capacitors). Calculations involving impedance frequently involve expressions similar to √(-1)/8, which simplify calculations and provide insights into circuit behavior.
2. Quantum Mechanics: Wave Functions
In quantum mechanics, wave functions, which describe the state of a quantum system, are often complex-valued functions. Operations on these wave functions frequently involve complex numbers, including terms analogous to √(-1)/8, contributing to the mathematical framework for predicting quantum phenomena.
3. Signal Processing: Fourier Transforms
Fourier transforms, widely used in signal processing, decompose signals into their constituent frequencies. These transforms often involve complex exponentials, leading to calculations that incorporate complex numbers, including fractions involving i, mirroring the structure of √(-1)/8.
4. Fluid Dynamics: Complex Potential
In fluid dynamics, the concept of complex potential simplifies the analysis of two-dimensional fluid flows. Complex potentials are functions of complex variables, and their manipulation frequently involves complex numbers similar in structure to √(-1)/8.
5. Fractal Geometry: Mandelbrot Set
The famous Mandelbrot set, a visually striking fractal, is defined using iterations of a complex quadratic polynomial. The generation of this set heavily relies on complex arithmetic operations, frequently involving expressions with imaginary components like √(-1)/8.
Conclusion: A Humble Expression with Profound Implications
While seemingly insignificant at first sight, √(-1)/8 serves as a powerful reminder of the profound implications of complex numbers. This seemingly simple expression opens doors to a richer mathematical landscape that finds applications across a diverse range of scientific and engineering fields. Its existence highlights the expansion of the number system beyond the realm of real numbers, allowing for the elegant solution of complex problems and a deeper understanding of the natural world. From analyzing AC circuits to deciphering the intricacies of quantum mechanics, the underlying principles embodied by √(-1)/8 contribute significantly to our mathematical and scientific understanding. The seemingly simple expression serves as a gateway to understanding a far more complex and fascinating universe. Further exploration into the intricacies of complex analysis reveals its versatility and its continued relevance in advanced mathematical applications. Its influence expands beyond pure mathematics into computational science, providing an essential foundation for solving complex equations and modelling intricate natural phenomena. It's a testament to the beauty and power of mathematical abstraction.
Latest Posts
Latest Posts
-
What Do Osmosis And Diffusion Have In Common
May 10, 2025
-
Living Things Are Based On A Universal Genetic Code
May 10, 2025
-
What Are The Angle Measures Of Triangle Abc
May 10, 2025
-
How To Solve Y 2x 3
May 10, 2025
-
Average Rate Of Change Vs Slope
May 10, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of -1 Over 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.