Solve This Inequality 3p 6 21
listenit
May 10, 2025 · 5 min read
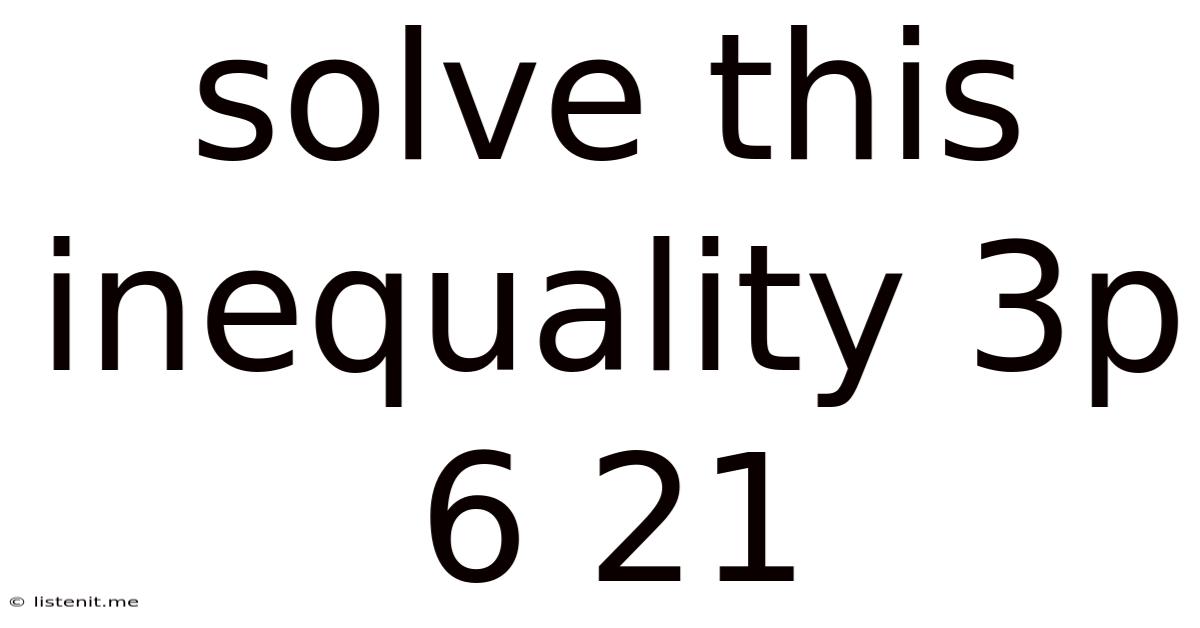
Table of Contents
Solving the Inequality: 3p + 6 ≤ 21 – A Comprehensive Guide
This article provides a comprehensive guide to solving the inequality 3p + 6 ≤ 21. We'll delve into the step-by-step process, explain the underlying principles, and explore various approaches to tackling similar inequalities. Understanding how to solve inequalities is crucial in various fields, from mathematics and engineering to economics and computer science. This guide will equip you with the knowledge and skills to confidently solve a wide range of linear inequalities.
Understanding Inequalities
Before diving into the solution, let's establish a firm understanding of inequalities. Unlike equations, which assert equality between two expressions, inequalities represent a relationship where one expression is greater than, less than, greater than or equal to, or less than or equal to another expression.
The symbols used to represent inequalities are:
- >: Greater than
- <: Less than
- ≥: Greater than or equal to
- ≤: Less than or equal to
Inequalities are powerful tools for modeling real-world scenarios involving constraints, limitations, or ranges of values. For instance, the speed limit on a highway can be represented as an inequality (speed ≤ 65 mph).
Solving Linear Inequalities: A Step-by-Step Approach
Solving the inequality 3p + 6 ≤ 21 involves isolating the variable 'p' to determine the range of values that satisfy the inequality. The process is similar to solving linear equations, but with a crucial difference: when multiplying or dividing by a negative number, you must reverse the inequality sign.
Step 1: Isolate the Term with the Variable
Our goal is to isolate the term containing 'p'. We begin by subtracting 6 from both sides of the inequality:
3p + 6 - 6 ≤ 21 - 6
This simplifies to:
3p ≤ 15
Step 2: Solve for the Variable
Next, we isolate 'p' by dividing both sides of the inequality by 3:
3p / 3 ≤ 15 / 3
This gives us:
p ≤ 5
Step 3: Interpreting the Solution
The solution, p ≤ 5, means that any value of 'p' that is less than or equal to 5 will satisfy the original inequality 3p + 6 ≤ 21. This can be represented graphically on a number line, where a closed circle at 5 indicates that 5 is included in the solution set, and the arrow extends to the left to encompass all values less than 5.
Graphical Representation of the Solution
Visualizing the solution set on a number line enhances understanding. The number line will show all possible values of 'p' that satisfy the inequality.
[Insert image here: A number line with a closed circle at 5 and an arrow pointing to the left, indicating all values less than or equal to 5.]
The closed circle at 5 indicates that 5 is included in the solution. The arrow extending to the left signifies that all values less than 5 are also part of the solution set.
Verifying the Solution
It's always good practice to verify the solution by substituting a value from the solution set into the original inequality. Let's try p = 4:
3(4) + 6 ≤ 21
12 + 6 ≤ 21
18 ≤ 21
This is true, confirming that our solution is correct. Let's also test a value outside the solution set, such as p = 6:
3(6) + 6 ≤ 21
18 + 6 ≤ 21
24 ≤ 21
This is false, further validating our solution.
Solving More Complex Inequalities
The principles outlined above can be extended to solve more complex inequalities. Let's consider some examples:
Example 1: Inequalities with Multiple Variables
Suppose we have the inequality: 2x + 3y ≤ 12. Solving for one variable in terms of the other requires similar steps:
- Subtract 2x from both sides: 3y ≤ 12 - 2x
- Divide both sides by 3: y ≤ 4 - (2/3)x
This solution expresses 'y' in terms of 'x', defining a region on a Cartesian plane.
Example 2: Inequalities with Parentheses
Consider the inequality: 2(x + 3) > 8.
- First, distribute the 2: 2x + 6 > 8
- Subtract 6 from both sides: 2x > 2
- Divide by 2: x > 1
This solution indicates that all values of 'x' greater than 1 satisfy the inequality.
Example 3: Inequalities with Fractions
Solving inequalities with fractions requires careful attention to the signs. Consider: (x/2) - 1 ≤ 3
- Add 1 to both sides: x/2 ≤ 4
- Multiply both sides by 2: x ≤ 8
Applications of Inequalities in Real World Scenarios
Inequalities are fundamental to numerous real-world applications:
- Budgeting: Determining how much you can spend on different items while staying within a budget.
- Production Planning: Calculating the maximum number of products that can be manufactured given resource constraints.
- Physics: Defining ranges of possible values for physical quantities like velocity or acceleration.
- Engineering: Ensuring that structural designs meet safety standards and load-bearing capacities.
- Economics: Modeling supply and demand, and optimizing resource allocation.
Common Mistakes to Avoid When Solving Inequalities
- Forgetting to Reverse the Inequality Sign: Remember to reverse the inequality sign when multiplying or dividing by a negative number. This is a crucial step that can easily lead to incorrect solutions.
- Incorrectly Combining Terms: Ensure you properly combine like terms on both sides of the inequality before isolating the variable.
- Errors in Arithmetic Operations: Double-check your calculations to avoid simple arithmetic errors that can affect the final solution.
- Neglecting to Check the Solution: Always verify your solution by substituting a value from the solution set into the original inequality.
Conclusion: Mastering Inequalities for Enhanced Problem-Solving
Solving inequalities is a fundamental skill in mathematics with wide-ranging applications. By understanding the underlying principles, following the step-by-step process, and practicing regularly, you can confidently tackle a broad range of inequality problems. Remember the importance of verifying your solutions and avoiding common pitfalls. Mastering inequalities will significantly enhance your problem-solving capabilities across various disciplines. This comprehensive guide provides a strong foundation for tackling more complex scenarios and real-world applications involving inequalities. Continue to practice and explore different types of inequalities to build your expertise.
Latest Posts
Latest Posts
-
A Container Of N2o3 Has A Pressure Of
May 10, 2025
-
What Is The Least Common Multiple Of 7 14
May 10, 2025
-
Find The Differential Dy Of The Given Function
May 10, 2025
-
Find The Lcm Of 12 And 15
May 10, 2025
-
Ground State Electron Configuration Of Cr
May 10, 2025
Related Post
Thank you for visiting our website which covers about Solve This Inequality 3p 6 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.