Solve For Y 3x 2y 6
listenit
May 13, 2025 · 5 min read
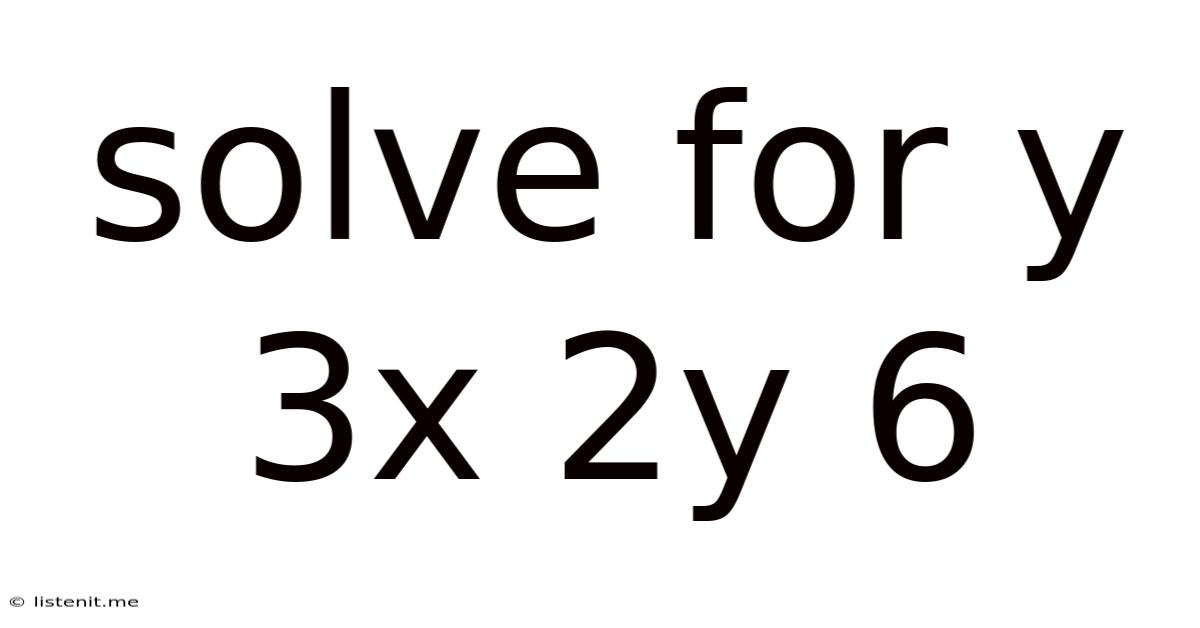
Table of Contents
Solving for y: A Comprehensive Guide to 3x + 2y = 6 and Beyond
This article provides a comprehensive guide to solving the equation 3x + 2y = 6 for y, explaining the process step-by-step and expanding on the broader concepts of algebraic manipulation and equation solving. We'll explore various methods, consider real-world applications, and delve into related topics to ensure a thorough understanding.
Understanding the Equation: 3x + 2y = 6
The equation 3x + 2y = 6 is a linear equation in two variables, x and y. This means that when graphed, it represents a straight line. The goal of "solving for y" is to rearrange the equation so that y is isolated on one side of the equals sign, expressed as a function of x. This allows us to easily determine the value of y for any given value of x.
Solving for y: Step-by-Step
The process of solving for y involves a series of algebraic manipulations, aiming to isolate y on one side of the equation. Here's a step-by-step breakdown:
-
Subtract 3x from both sides:
The first step is to eliminate the x term from the left-hand side of the equation. We achieve this by subtracting 3x from both sides, maintaining the balance of the equation:
3x + 2y - 3x = 6 - 3x
This simplifies to:
2y = 6 - 3x
-
Divide both sides by 2:
Now, we need to isolate y. Since y is multiplied by 2, we divide both sides of the equation by 2:
2y / 2 = (6 - 3x) / 2
This simplifies to:
y = (6 - 3x) / 2
-
Simplify (Optional):
While the equation is solved, we can simplify the expression further by dividing each term within the parenthesis by 2:
y = 3 - (3/2)x
Or, equivalently:
y = - (3/2)x + 3
This final equation, y = -(3/2)x + 3, is the solution for y in terms of x. It's in the slope-intercept form (y = mx + b), where m represents the slope (-3/2) and b represents the y-intercept (3).
Graphical Representation and Interpretation
The equation y = -(3/2)x + 3 represents a straight line on a Cartesian coordinate system. The slope of -3/2 indicates that for every 2 units increase in x, y decreases by 3 units. The y-intercept of 3 means the line crosses the y-axis at the point (0, 3). Graphing this line visually helps to understand the relationship between x and y.
Practical Applications
Solving linear equations like 3x + 2y = 6 has wide-ranging applications in various fields:
-
Economics: Linear equations are fundamental in economic modeling. They can represent supply and demand curves, production functions, or budget constraints. Solving for a specific variable allows economists to analyze the impact of changes in one variable on another.
-
Physics: In physics, linear equations are used extensively to model physical phenomena. For example, they can describe the relationship between distance, speed, and time, or the relationship between force, mass, and acceleration (Newton's second law).
-
Engineering: Engineers use linear equations to model and solve problems in various fields, including structural analysis, circuit design, and fluid mechanics. Solving for specific variables helps engineers optimize designs and predict system behavior.
-
Computer Science: Linear equations are crucial in computer graphics, image processing, and machine learning algorithms. Solving these equations allows for efficient manipulation and transformation of data.
-
Business and Finance: Linear equations can model profit margins, cost analysis, and financial projections. Solving for specific variables helps businesses make informed decisions regarding pricing, resource allocation, and investment strategies.
Expanding on Algebraic Techniques
Solving for y in 3x + 2y = 6 involves basic algebraic manipulations. Understanding these techniques is essential for tackling more complex equations. Here are some key concepts:
-
Addition and Subtraction Property of Equality: You can add or subtract the same quantity from both sides of an equation without changing its equality. This was used in the first step of our solution.
-
Multiplication and Division Property of Equality: You can multiply or divide both sides of an equation by the same non-zero quantity without changing its equality. This was applied in the second step.
-
Distributive Property: This property states that a(b + c) = ab + ac. This is crucial when dealing with equations involving parentheses.
-
Combining Like Terms: This involves simplifying expressions by adding or subtracting terms that have the same variable and exponent.
-
Order of Operations (PEMDAS/BODMAS): Remember to follow the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) when simplifying expressions.
Solving More Complex Equations
The principles used to solve 3x + 2y = 6 can be extended to solve more complex linear equations involving multiple variables and more intricate expressions. For instance, consider the equation:
5x + 2y - 7 = 3x + 4y + 1
Solving for y involves a similar process:
-
Combine like terms: Rearrange the equation to group x terms and y terms together. This would give you 2x - 2y = 8
-
Isolate the y term: Subtract 2x from both sides to isolate the terms involving y. This results in -2y = -2x + 8
-
Solve for y: Divide both sides of the equation by -2. This provides the final solution: y = x - 4
Beyond Linear Equations: A Glimpse into Other Equation Types
While this article focuses on linear equations, it's crucial to understand that other types of equations exist, each requiring different solution methods:
-
Quadratic Equations: These equations involve terms with x², requiring techniques like factoring, the quadratic formula, or completing the square to solve.
-
Cubic Equations: These equations involve terms with x³. Solving cubic equations can be more complex and might involve numerical methods.
-
Exponential Equations: These equations involve variables as exponents, often solved using logarithms.
-
Logarithmic Equations: These equations involve logarithmic functions, solved by using exponential properties.
-
Trigonometric Equations: These equations involve trigonometric functions (sine, cosine, tangent, etc.), requiring trigonometric identities and techniques.
Conclusion
Solving for y in the equation 3x + 2y = 6 provides a foundational understanding of algebraic manipulation and equation solving. The step-by-step process and its practical applications demonstrate the importance of these skills across various disciplines. By grasping the fundamental principles of algebraic operations and expanding into more complex equation types, you'll develop a strong foundation for advanced mathematical problem-solving. Remember to practice regularly to solidify your understanding and improve your proficiency in solving equations efficiently.
Latest Posts
Latest Posts
-
How To Do Linear Regression On A Calculator
May 13, 2025
-
A Sample Of Helium Gas Occupies 12 9
May 13, 2025
-
In A Polar Covalent Bond Electrons Are Shared
May 13, 2025
-
Is Oil Polar Or Non Polar
May 13, 2025
-
What Is The Derivative Of 3e X
May 13, 2025
Related Post
Thank you for visiting our website which covers about Solve For Y 3x 2y 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.