Solve For Y 1 3x Y 4
listenit
May 09, 2025 · 5 min read
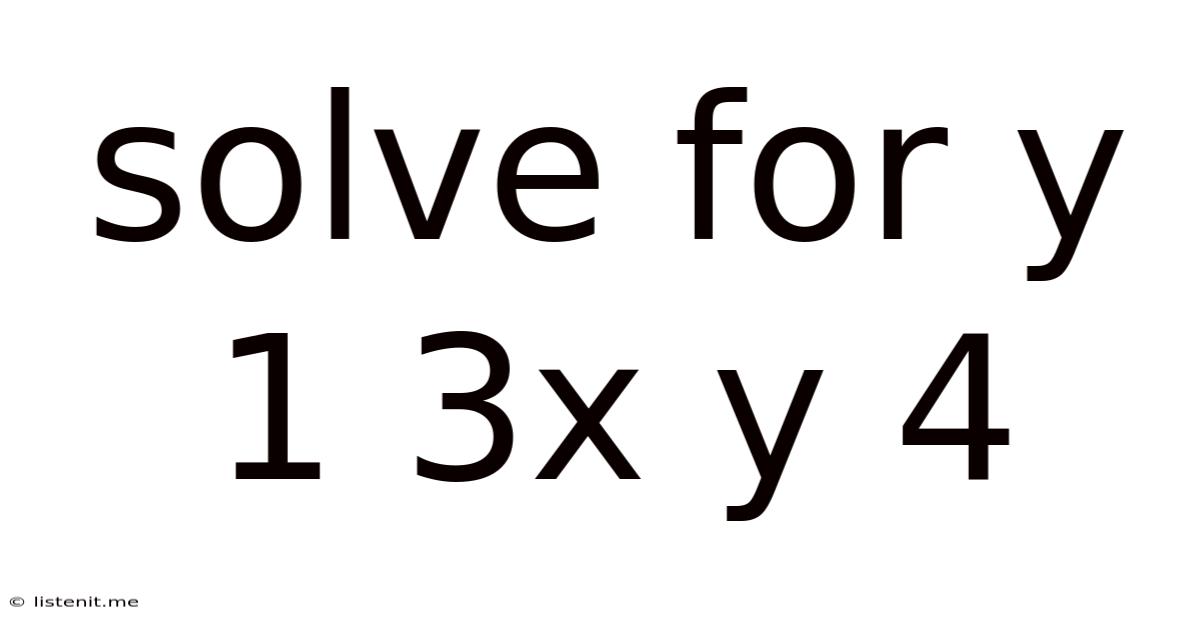
Table of Contents
Solving for y: A Comprehensive Guide to 1/3x + y = 4
This article provides a comprehensive guide on how to solve for y in the equation 1/3x + y = 4. We'll cover the fundamental algebraic principles involved, walk through the solution step-by-step, explore variations of this equation, and discuss practical applications. By the end, you'll not only understand how to solve this specific equation but also possess the skills to tackle similar algebraic problems with confidence.
Understanding the Equation: 1/3x + y = 4
The equation 1/3x + y = 4 represents a linear equation in two variables, x and y. This means its graph is a straight line. The goal of "solving for y" is to isolate y on one side of the equation, expressing it in terms of x. This gives us the equation in slope-intercept form (y = mx + b), where 'm' represents the slope and 'b' represents the y-intercept. This form is incredibly useful for graphing the line and understanding its properties.
Step-by-Step Solution: Isolating y
To solve for y, we need to manipulate the equation using algebraic operations. Remember that whatever we do to one side of the equation, we must do to the other side to maintain balance. Here's the step-by-step process:
-
Identify the term with y: In the equation 1/3x + y = 4, the term with y is simply y.
-
Isolate the y term: To isolate y, we need to move the 1/3x term to the right side of the equation. We can do this by subtracting 1/3x from both sides:
y = 4 - 1/3x
-
Rewrite in slope-intercept form: While the equation is solved for y, it's conventionally written in slope-intercept form (y = mx + b). Rearranging the terms, we get:
y = -1/3x + 4
Therefore, the solution for y is y = -1/3x + 4. This equation tells us that for any given value of x, we can calculate the corresponding value of y.
Understanding the Solution: Slope and y-intercept
The solution, y = -1/3x + 4, is in the slope-intercept form (y = mx + b), where:
-
m = -1/3 is the slope: The slope represents the rate of change of y with respect to x. A slope of -1/3 indicates that for every 3-unit increase in x, y decreases by 1 unit. The negative sign signifies a negative correlation – as x increases, y decreases.
-
b = 4 is the y-intercept: The y-intercept is the point where the line crosses the y-axis (where x = 0). In this case, the line intersects the y-axis at the point (0, 4).
Graphing the Equation
Plotting the equation y = -1/3x + 4 on a coordinate plane provides a visual representation of the relationship between x and y. The y-intercept (0, 4) gives us one point. To find another point, we can choose any value for x and calculate the corresponding y value. For instance:
- If x = 3, then y = -1/3(3) + 4 = 3
- If x = -3, then y = -1/3(-3) + 4 = 5
This gives us the points (3, 3) and (-3, 5). Plotting these points and drawing a line through them gives us the graph of the equation.
Variations and Extensions
The basic principle of solving for y applies to many similar equations. Let's explore some variations:
1. Equations with more complex terms: Consider the equation 2x + 3y = 6. The steps to solve for y are:
- Subtract 2x from both sides: 3y = 6 - 2x
- Divide both sides by 3: y = 2 - (2/3)x
- Rewrite in slope-intercept form: y = -(2/3)x + 2
2. Equations with fractions: Solving equations with fractions requires careful manipulation. For example:
(x/2) + (y/3) = 1
- Multiply both sides by 6 (the least common multiple of 2 and 3) to eliminate the fractions: 3x + 2y = 6
- Subtract 3x from both sides: 2y = 6 - 3x
- Divide by 2: y = 3 - (3/2)x
- Rewrite in slope-intercept form: y = -(3/2)x + 3
3. Equations with parentheses: Equations involving parentheses require expanding them before solving for y. For example:
2(x + y) = 8
- Expand the parentheses: 2x + 2y = 8
- Subtract 2x from both sides: 2y = 8 - 2x
- Divide by 2: y = 4 - x
- Rewrite in slope-intercept form: y = -x + 4
Real-World Applications
Linear equations, such as the one we solved, have numerous applications in various fields:
-
Economics: Supply and demand curves are often represented by linear equations. Solving for y (quantity demanded or supplied) allows economists to analyze market equilibrium.
-
Physics: Linear equations describe many physical phenomena, such as velocity, acceleration, and the relationship between force and displacement.
-
Engineering: Linear equations are used in structural analysis, circuit design, and many other engineering applications.
-
Finance: Linear equations are employed in calculating simple interest, depreciation, and other financial calculations.
Troubleshooting Common Mistakes
When solving for y, several common mistakes can occur:
-
Incorrectly applying the order of operations: Remember to follow the order of operations (PEMDAS/BODMAS).
-
Errors in signs: Carefully manage positive and negative signs when adding, subtracting, multiplying, or dividing.
-
Errors in fraction manipulation: Be meticulous when working with fractions, ensuring you correctly find common denominators and simplify expressions.
Conclusion
Solving for y in the equation 1/3x + y = 4, resulting in y = -1/3x + 4, is a fundamental algebraic skill with broad applications. Understanding the process, the meaning of slope and y-intercept, and the ability to apply this to variations of the equation are crucial for success in algebra and many other quantitative fields. Remember to practice consistently, focusing on accuracy and understanding the underlying principles, to master this important skill. By following the step-by-step solutions and paying attention to potential pitfalls, you can confidently solve for y in various linear equations and unlock a deeper understanding of algebraic concepts.
Latest Posts
Latest Posts
-
What Is The Exact Value Of Cos 195
May 10, 2025
-
7 Minus The Product Of 3 And X
May 10, 2025
-
Granulation Is Evidence Of What Phenomenon
May 10, 2025
-
How Many Electrons Can The 5th Shell Hold
May 10, 2025
-
Graph The Line 2x Y 4
May 10, 2025
Related Post
Thank you for visiting our website which covers about Solve For Y 1 3x Y 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.