Solve For The Variable In 7 28 25 X
listenit
May 09, 2025 · 5 min read
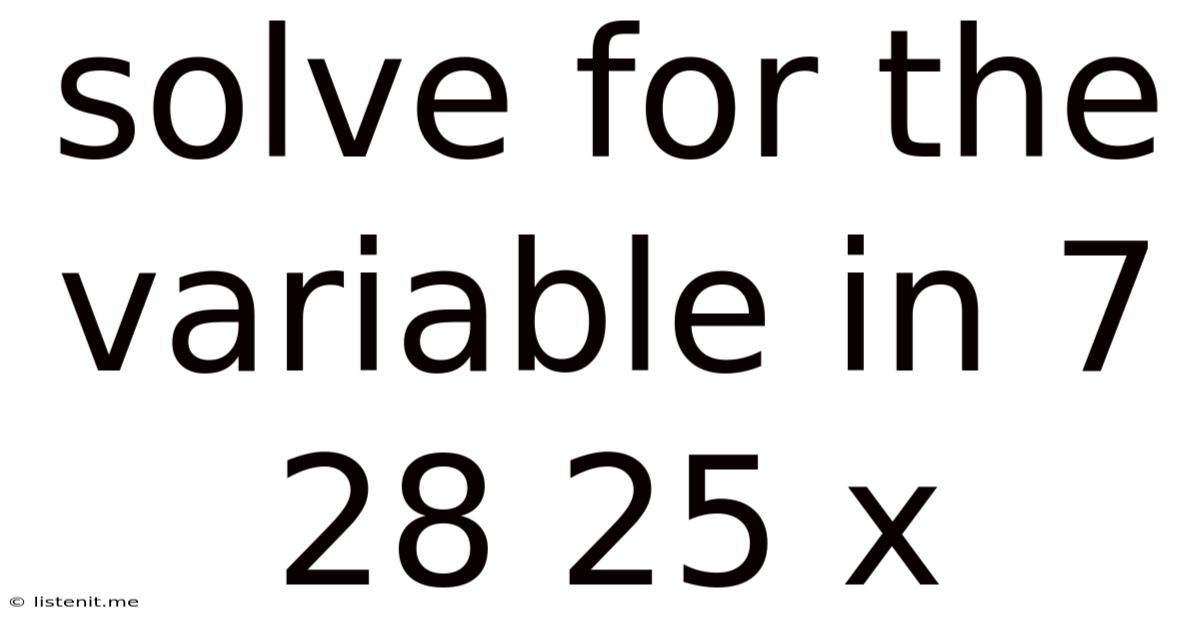
Table of Contents
Solving for the Variable: Unveiling the Mystery of 7, 28, 25, x
This article delves into the intriguing mathematical puzzle presented by the sequence 7, 28, 25, x. We'll explore various approaches to solving for the variable 'x', examining different mathematical relationships and patterns that might underlie this sequence. We'll also discuss the importance of identifying patterns in problem-solving and the value of exploring multiple potential solutions. Understanding the underlying logic is crucial not just for finding the answer, but for developing stronger mathematical reasoning skills.
Identifying Potential Patterns: The Foundation of Problem Solving
The key to solving this puzzle lies in identifying the relationship between the numbers 7, 28, and 25. There's no single obvious pattern, which is what makes this problem so engaging. We need to consider several possibilities:
1. Arithmetic Sequences: Adding and Subtracting
One common approach is to look for arithmetic sequences – where a constant value is added or subtracted to obtain the next number in the sequence. Let's investigate:
- Difference between consecutive terms: 28 - 7 = 21; 25 - 28 = -3. There's no consistent difference, ruling out a simple arithmetic progression.
2. Geometric Sequences: Multiplication and Division
Next, we explore geometric sequences, where each term is obtained by multiplying or dividing the previous term by a constant value. Again, let's investigate:
- Ratio between consecutive terms: 28 / 7 = 4; 25 / 28 ≈ 0.89. No consistent ratio exists, eliminating a simple geometric progression.
3. Quadratic Relationships: Exploring Second-Order Patterns
A more complex approach involves considering quadratic relationships. This might involve a pattern where the differences between consecutive terms themselves form an arithmetic sequence. Let's analyze the differences again:
- First differences: 28 - 7 = 21; 25 - 28 = -3
- Second differences: -3 - 21 = -24
The lack of a consistent second difference suggests that a simple quadratic relationship isn't directly apparent.
4. Combinations of Operations: A More Nuanced Approach
Given the lack of simple arithmetic or geometric patterns, we might need to explore more complex combinations of operations. This might include a combination of addition, subtraction, multiplication, or division. It is important to consider several hypotheses before settling on a solution. Here are a couple of possibilities:
-
Hypothesis 1: Alternating Operations: Could the pattern involve alternating between two different operations? For instance, multiplying by a factor and then subtracting a value? Let's explore this possibility.
-
Hypothesis 2: Hidden Relationship: Is there a less obvious relationship, such as a connection to prime numbers, perfect squares, or other mathematical concepts? This requires a more in-depth mathematical analysis and creative thinking.
Exploring the Possibilities: A Deeper Dive
Let's further explore some potential patterns and relationships which could explain the sequence 7, 28, 25, x. This will entail a combination of methodical investigation and intuition.
Analyzing the Numbers Themselves: Prime Factorization and Other Properties
A powerful approach is to break down each number into its prime factors:
- 7: 7 (a prime number)
- 28: 2 x 2 x 7
- 25: 5 x 5
Notice that 7 is a common factor in both 7 and 28. Could this be significant? Also, 25 is a perfect square (5²). The presence of a prime number, a composite number with a prime factor, and a perfect square might suggest a pattern based on number theory properties.
Exploring Number Theory Concepts: Expanding the Search
Let's consider some concepts from number theory which might offer insights:
-
Perfect Squares and Cubes: The presence of 25 (a perfect square) might point to a pattern involving perfect squares or cubes.
-
Prime Numbers: The prime number 7 appears in the first two terms. Are there any connections between 7 and the subsequent numbers?
-
Modular Arithmetic: This branch of number theory deals with remainders after division. Could there be a consistent remainder when each number is divided by a specific value?
The Importance of Context: Missing Information
It's important to remember that without additional context or information, there might be multiple valid solutions. The sequence might be part of a larger, more complex pattern that isn't immediately apparent. A seemingly simple number sequence can often have surprisingly sophisticated underlying structures.
Developing Problem-Solving Strategies: A Step-by-Step Approach
The challenge of solving for 'x' emphasizes the importance of a structured approach to problem-solving. Let's summarize effective strategies:
-
Careful Observation: Begin by carefully examining the numbers in the sequence. Look for obvious patterns (arithmetic, geometric, etc.).
-
Systematic Analysis: Explore different types of sequences, including arithmetic, geometric, and quadratic relationships. Don't overlook more complex combinations of operations.
-
Number Theory Exploration: Consider applying concepts from number theory, such as prime factorization, perfect squares, modular arithmetic, etc.
-
Creative Thinking: If standard methods fail, allow for creative thinking and exploration of unconventional patterns. There might be multiple valid solutions.
-
Hypothesis Testing: Formulate hypotheses about the potential underlying pattern. Test these hypotheses using the known terms.
-
Iterative Refinement: If your initial hypotheses don't work, refine them based on the results of your tests.
-
Consider Context: Remember that the context of the problem might provide additional clues.
Conclusion: The Power of Mathematical Exploration
The seemingly simple sequence 7, 28, 25, x offers a compelling illustration of the power of mathematical exploration. Solving for 'x' isn't just about finding a numerical answer; it's about developing stronger problem-solving skills, fostering critical thinking, and appreciating the richness and complexity of mathematics.
While a definitive solution without additional context remains elusive, the process of exploring different approaches is what makes this puzzle so rewarding. It challenges us to move beyond rote calculation and to engage with the underlying structure and logic of mathematical relationships. The quest to solve for 'x' is a journey of discovery—a testament to the enduring fascination of mathematical puzzles. The exercise itself sharpens our analytical skills and enhances our appreciation for the elegant patterns that underpin the mathematical world. This demonstrates how a seemingly simple problem can lead to significant growth in understanding and mathematical reasoning.
Latest Posts
Latest Posts
-
44 Out Of 50 Is What Percent
May 09, 2025
-
What Is The Gcf Of 45 And 60
May 09, 2025
-
What Does The Root Word Troph Mean
May 09, 2025
-
Can A Rational Number Be An Integer
May 09, 2025
-
Rounding To The Nearest Quarter Hour
May 09, 2025
Related Post
Thank you for visiting our website which covers about Solve For The Variable In 7 28 25 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.