Simplify X 2 Xy Y 2
listenit
May 09, 2025 · 5 min read
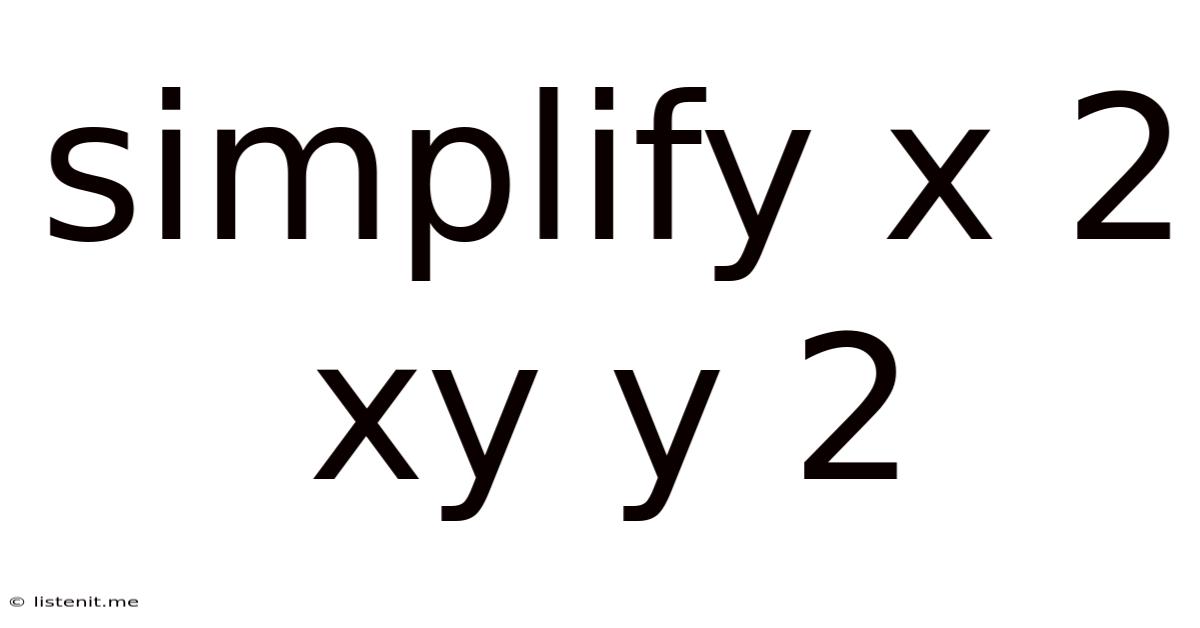
Table of Contents
Simplifying x² + 2xy + y²: A Comprehensive Guide
The expression x² + 2xy + y² is a fundamental concept in algebra, appearing frequently in various mathematical contexts. Understanding its simplification and applications is crucial for success in algebra and beyond. This comprehensive guide will delve into the simplification process, explore its geometrical interpretation, discuss its applications in different areas of mathematics, and provide practical examples to solidify your understanding.
Understanding the Expression
The expression x² + 2xy + y² represents a trinomial, which is a polynomial with three terms. Each term consists of variables (x and y) raised to certain powers, multiplied by coefficients. Specifically, we have:
- x²: x squared (x multiplied by itself)
- 2xy: Two times x multiplied by y
- y²: y squared (y multiplied by itself)
The key to simplifying this expression lies in recognizing its special form.
Factoring the Trinomial: The Perfect Square Trinomial
The expression x² + 2xy + y² is a classic example of a perfect square trinomial. A perfect square trinomial is a trinomial that can be factored into the square of a binomial. In other words, it can be expressed in the form (a + b)².
The general form of a perfect square trinomial is: a² + 2ab + b² = (a + b)²
In our case:
a = x b = y
Therefore, x² + 2xy + y² can be factored as:
(x + y)²
This means that x² + 2xy + y² is equivalent to (x + y) multiplied by itself.
Proof through Expansion
To verify this factorization, we can expand (x + y)² using the FOIL method (First, Outer, Inner, Last):
(x + y)(x + y) = x² + xy + xy + y² = x² + 2xy + y²
This confirms that our factorization is correct.
Geometrical Interpretation
The perfect square trinomial x² + 2xy + y² has a clear geometrical interpretation. Imagine a square with sides of length (x + y). The area of this square is (x + y)².
This square can be divided into four smaller regions:
- A square with side x, having an area of x²
- A square with side y, having an area of y²
- Two rectangles, each with sides x and y, each having an area of xy.
The total area of the large square is the sum of the areas of these four smaller regions: x² + xy + xy + y² = x² + 2xy + y². This visually demonstrates the equivalence of (x + y)² and x² + 2xy + y².
Applications in Mathematics
The simplification of x² + 2xy + y² to (x + y)² has numerous applications across various mathematical fields:
1. Algebra: Solving Equations and Inequalities
Recognizing perfect square trinomials significantly simplifies solving quadratic equations and inequalities. For example, consider the equation:
x² + 6x + 9 = 0
This is a perfect square trinomial, as it can be factored as (x + 3)². Therefore, the equation becomes:
(x + 3)² = 0
Solving for x, we get x = -3.
2. Calculus: Differentiation and Integration
The simplification can streamline differentiation and integration processes. For instance, finding the derivative of (x + y)² is much simpler than finding the derivative of x² + 2xy + y² directly, especially if x and y are functions of another variable.
3. Geometry: Area Calculations
As illustrated in the geometrical interpretation, understanding this factorization is crucial for calculating areas of squares and rectangles involving algebraic expressions.
4. Trigonometry: Trigonometric Identities
The concept extends to trigonometric identities. Certain trigonometric expressions can be manipulated into perfect square trinomial forms, enabling simplification and solution of trigonometric equations.
5. Number Theory: Perfect Squares and Factorization
The concept is fundamental in number theory. Recognizing perfect square trinomials helps in identifying perfect squares and simplifies the factorization of polynomials.
Advanced Applications and Extensions
The concept extends beyond simple algebraic manipulation.
Completing the Square
The process of completing the square relies heavily on the understanding of perfect square trinomials. This technique is essential for solving quadratic equations that cannot be easily factored, and it forms the basis for deriving the quadratic formula.
Polynomial Division and Remainder Theorem
When dividing polynomials, recognizing perfect square trinomials can simplify the process and help in determining the remainder using the Remainder Theorem.
Partial Fraction Decomposition
In calculus, partial fraction decomposition often involves factoring the denominator into simpler terms. Recognizing perfect square trinomials can greatly simplify this process.
Practical Examples
Let's work through some examples to solidify our understanding:
Example 1: Simplify 4x² + 12xy + 9y²
This is a perfect square trinomial with a = 2x and b = 3y. Therefore, it simplifies to (2x + 3y)².
Example 2: Solve the equation x² + 4x + 4 = 25
This equation can be rewritten as (x + 2)² = 25. Taking the square root of both sides gives x + 2 = ±5. Solving for x, we get x = 3 or x = -7.
Example 3: Find the area of a square with sides of length (3a + 2b).
The area is (3a + 2b)², which expands to 9a² + 12ab + 4b².
Example 4: Differentiate f(x) = (x + 5)²
Using the chain rule, the derivative is f'(x) = 2(x + 5).
These examples showcase the broad applicability of understanding and simplifying x² + 2xy + y².
Conclusion
The seemingly simple expression x² + 2xy + y² holds significant importance in mathematics. Understanding its simplification to (x + y)² is a fundamental skill, opening doors to a deeper understanding of various mathematical concepts and their applications. From solving equations and simplifying expressions to calculating areas and applying in calculus, the ability to recognize and utilize perfect square trinomials is a valuable asset in any mathematical endeavor. Mastering this concept builds a solid foundation for more advanced mathematical studies. Remember to practice regularly and explore the diverse applications to strengthen your comprehension and proficiency.
Latest Posts
Latest Posts
-
Who Is Known As The Father Of Texas
May 09, 2025
-
What Is The Difference Between A Structural And Molecular Formula
May 09, 2025
-
A Sound Wave Is An Example Of A
May 09, 2025
-
Write 39 100 As A Decimal Number
May 09, 2025
-
3 Less Than The Product Of 8 And A Number
May 09, 2025
Related Post
Thank you for visiting our website which covers about Simplify X 2 Xy Y 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.