Seven Less Than Four Times A Number
listenit
May 12, 2025 · 4 min read
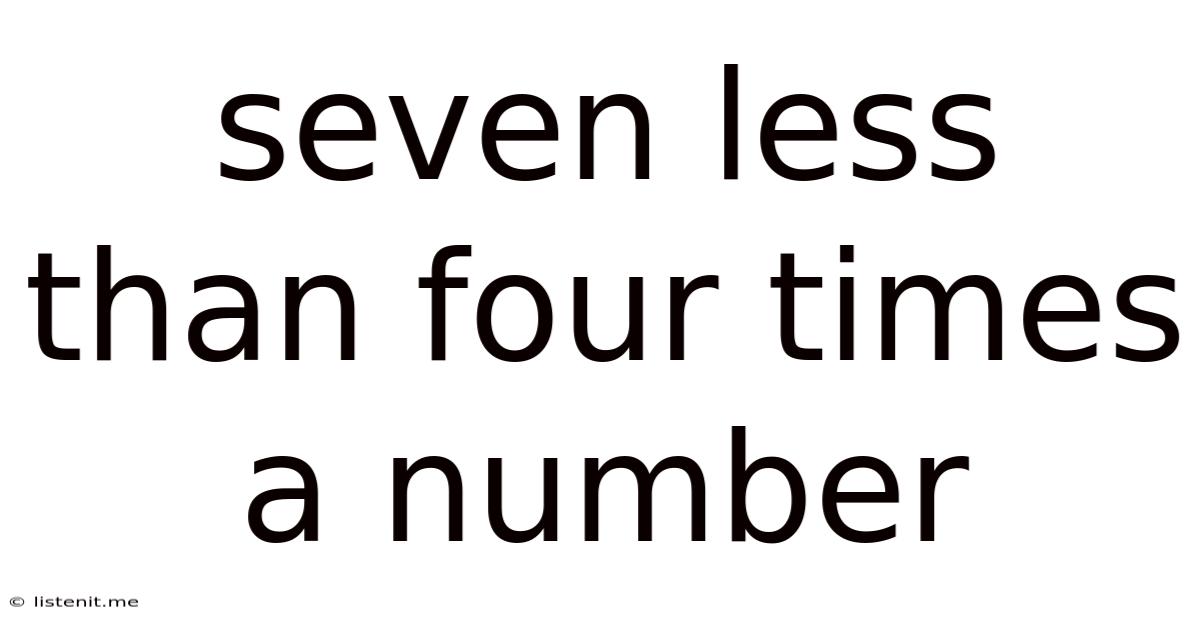
Table of Contents
Seven Less Than Four Times a Number: A Deep Dive into Algebraic Expressions
The seemingly simple phrase "seven less than four times a number" holds a wealth of mathematical possibilities, encompassing fundamental algebraic concepts, practical applications, and even extensions into more advanced mathematical territories. This article will explore this expression in detail, examining its translation into algebraic notation, its manipulation within equations and inequalities, its use in real-world problem-solving, and its connection to broader mathematical ideas.
Understanding the Expression: From Words to Algebra
The phrase "seven less than four times a number" is a verbal description of an algebraic expression. Let's break it down step-by-step:
-
"A number": This represents an unknown quantity, typically denoted by a variable, most commonly x. However, any letter can be used.
-
"Four times a number": This translates directly to 4x (or 4x). Multiplication is implied by the word "times."
-
"Seven less than": This indicates subtraction. "Seven less than" something means that 7 is subtracted from that something. Therefore, "seven less than four times a number" becomes 4x - 7.
Therefore, the complete algebraic representation of the phrase is 4x - 7. This is a linear expression, meaning the highest power of the variable is 1.
Manipulating the Expression: Equations and Inequalities
The expression 4x - 7 forms the foundation for various equations and inequalities. Let's explore a few examples:
Equations: Finding the Value of 'x'
An equation sets the expression equal to a specific value. For instance:
-
4x - 7 = 17: To solve for x, we follow these steps:
- Add 7 to both sides: 4x = 24
- Divide both sides by 4: x = 6
Therefore, in this equation, the number is 6.
Let's try another example:
-
4x - 7 = -1: Following the same steps:
- Add 7 to both sides: 4x = 6
- Divide both sides by 4: x = 1.5 or 3/2
Here, the number is 1.5.
Inequalities: Defining a Range of Values
Inequalities use symbols like < (less than), > (greater than), ≤ (less than or equal to), and ≥ (greater than or equal to) to define a range of values for x. For example:
-
4x - 7 > 10:
- Add 7 to both sides: 4x > 17
- Divide both sides by 4: x > 4.25
This inequality indicates that the number is greater than 4.25.
-
4x - 7 ≤ 0:
- Add 7 to both sides: 4x ≤ 7
- Divide both sides by 4: x ≤ 1.75
This inequality shows that the number is less than or equal to 1.75.
Real-World Applications: Putting it into Practice
The expression "seven less than four times a number" isn't just an abstract algebraic concept; it has practical applications in various real-world scenarios. Let's consider a few examples:
Scenario 1: Profit Calculation
Imagine a small business selling handmade crafts. Each craft sells for $4, and the fixed costs (rent, utilities, etc.) are $7. The profit (P) can be represented by the equation:
P = 4x - 7, where x is the number of crafts sold.
This equation directly uses the expression we've been discussing. To determine the profit after selling 10 crafts, we substitute x = 10:
P = 4(10) - 7 = 33
The profit would be $33.
Scenario 2: Temperature Conversion
While not a direct representation, the concept is similar. Suppose you're working with a temperature scale where the conversion from one scale to another involves multiplying by 4 and subtracting 7. The expression would directly model this conversion.
Scenario 3: Geometry Problems
Consider a rectangle where the length is four times the width minus seven units. If we let 'w' represent the width, the length 'l' can be expressed as:
l = 4w - 7
This equation uses the expression to relate the length and width of the rectangle. Given a certain width, you can calculate the length using this equation.
Expanding the Concept: Beyond Linear Expressions
The expression 4x - 7 provides a foundation for understanding more complex mathematical concepts.
Quadratic Equations: Introducing the Square
By adding a squared term, we can create a quadratic equation:
4x² - 7 = 0 or 4x² - 7 = 17 or any other equation setting the expression equal to a value
Solving quadratic equations involves more advanced techniques, like factoring, completing the square, or using the quadratic formula.
Higher-Order Polynomials: More Complex Relationships
Further extending this, we can incorporate even higher powers of x, leading to cubic, quartic, or higher-order polynomial expressions. These higher-order expressions represent more complex relationships between variables.
Systems of Equations: Multiple Variables
We can also integrate the expression into a system of equations, involving multiple variables and multiple equations. This would require techniques like substitution or elimination to find solutions.
Conclusion: The Power of a Simple Expression
The seemingly simple phrase "seven less than four times a number," when translated into the algebraic expression 4x - 7, unlocks a world of mathematical possibilities. From solving basic equations and inequalities to modeling real-world situations and venturing into more advanced mathematical territories, this expression serves as a fundamental building block for understanding and applying algebraic concepts. Its versatility highlights the power of algebraic representation and its importance in various fields. By understanding and manipulating this expression, we gain valuable insights into the core principles of algebra and their applications in the world around us. Mastering this seemingly simple concept lays a strong foundation for tackling more complex mathematical challenges.
Latest Posts
Latest Posts
-
What Is 45 As A Decimal
May 12, 2025
-
Which Of The Following Best Compares Linnaean Taxonomy With Cladistics
May 12, 2025
-
Area Of A Circle With A Diameter Of 16 Feet
May 12, 2025
-
How Does Water Shape Earths Surface
May 12, 2025
-
9 To 3 To 3 To 1 Ratio
May 12, 2025
Related Post
Thank you for visiting our website which covers about Seven Less Than Four Times A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.