Lowest Common Factor Of 7 And 9
listenit
Mar 28, 2025 · 5 min read
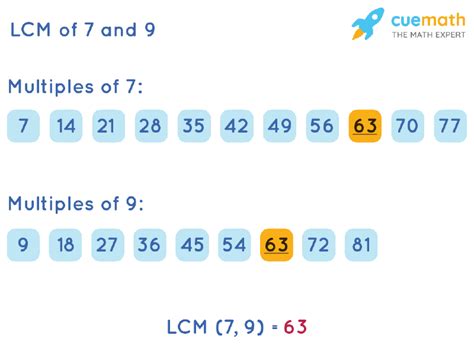
Table of Contents
Unveiling the Secrets of the Lowest Common Factor: A Deep Dive into 7 and 9
Finding the lowest common factor (LCF) might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a world of mathematical elegance and practical applications. This comprehensive guide will explore the LCF of 7 and 9, providing a step-by-step explanation, exploring related mathematical concepts, and demonstrating its relevance in various fields.
Understanding the Fundamentals: Factors and Multiples
Before diving into the LCF of 7 and 9, let's establish a strong foundation by defining key terms:
-
Factors: Factors are numbers that divide evenly into a given number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.
-
Multiples: Multiples are numbers obtained by multiplying a given number by any integer. For instance, multiples of 5 are 5, 10, 15, 20, and so on.
-
Common Factors: These are factors shared by two or more numbers. For example, the common factors of 12 and 18 are 1, 2, 3, and 6.
-
Lowest Common Factor (LCF): Also known as the Greatest Common Divisor (GCD), the LCF is the largest number that divides evenly into all the given numbers without leaving a remainder. It's the highest common factor among the set of numbers.
Finding the LCF of 7 and 9: A Practical Approach
Now, let's focus on finding the LCF of 7 and 9. Since 7 and 9 are relatively prime numbers, meaning they share no common factors other than 1, their LCF is simply 1.
Let's illustrate this with a few methods:
1. Listing Factors Method
This is a straightforward approach, especially for smaller numbers:
- Factors of 7: 1, 7
- Factors of 9: 1, 3, 9
Comparing the two lists, we observe that the only common factor is 1. Therefore, the LCF of 7 and 9 is 1.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves expressing each number as a product of its prime factors:
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 9: 3 x 3 = 3²
Since there are no common prime factors between 7 and 9, their LCF is 1.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCD (and therefore the LCF) of two numbers. It's particularly useful for larger numbers where listing factors becomes cumbersome. The algorithm involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Let's apply it to 7 and 9:
- Divide the larger number (9) by the smaller number (7): 9 ÷ 7 = 1 with a remainder of 2.
- Replace the larger number with the smaller number (7) and the smaller number with the remainder (2): 7 ÷ 2 = 3 with a remainder of 1.
- Repeat: 2 ÷ 1 = 2 with a remainder of 0.
The last non-zero remainder is 1, so the GCD (and LCF) of 7 and 9 is 1.
Beyond the Basics: Exploring Related Concepts
Understanding the LCF of 7 and 9 provides a springboard to explore more advanced mathematical concepts:
Relatively Prime Numbers
As demonstrated, 7 and 9 are relatively prime numbers, meaning their greatest common divisor (GCD) is 1. This implies they share no common factors other than 1. This concept is crucial in various areas of mathematics, including number theory and cryptography.
Applications in Real-World Scenarios
While seemingly abstract, the concept of LCF has practical applications:
-
Scheduling: Imagine planning events that occur at different intervals. Finding the LCF can help determine when the events will coincide.
-
Fraction Simplification: The LCF is essential for simplifying fractions to their lowest terms. Dividing both the numerator and denominator by their LCF reduces the fraction to its simplest form.
-
Measurement and Conversion: The LCF plays a role in converting units of measurement, ensuring accurate calculations.
Expanding the Understanding: Lowest Common Multiple (LCM)
While we've focused on the LCF, it's essential to understand its counterpart – the Lowest Common Multiple (LCM). The LCM is the smallest positive integer that is a multiple of all the given numbers.
For 7 and 9:
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63…
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63…
The smallest common multiple is 63.
There's a relationship between the LCF and LCM:
LCM(a, b) * GCD(a, b) = a * b
Applying this to 7 and 9:
LCM(7, 9) * GCD(7, 9) = 7 * 9
63 * 1 = 63
This formula provides a convenient way to calculate the LCM if the GCD is known.
Advanced Applications: Number Theory and Cryptography
The concepts of LCF and LCM are fundamental building blocks in number theory, a branch of mathematics dealing with the properties of integers. They have significant applications in cryptography, the practice of secure communication in the presence of adversarial behavior.
Euclidean Algorithm and Cryptography
The Euclidean algorithm, mentioned earlier, plays a crucial role in various cryptographic algorithms. It is used to find modular inverses, a critical component in encryption and decryption processes. These inverses are essential for secure key exchange and data protection.
Prime Numbers and Security
The concept of relatively prime numbers, directly linked to the LCF, underpins many encryption techniques. The security of these systems often relies on the difficulty of factoring large numbers into their prime factors, a computationally intensive task.
Conclusion: The Significance of Simple Concepts
While the LCF of 7 and 9 might appear trivial at first glance, exploring it has unveiled a wealth of mathematical concepts and real-world applications. From understanding factors and multiples to delving into relatively prime numbers and their role in cryptography, this journey has highlighted the interconnectedness of seemingly simple mathematical ideas and their profound impact on various fields. The ability to grasp these fundamental concepts forms a strong foundation for further exploration of advanced mathematical topics and their practical applications in diverse disciplines. The seemingly simple task of finding the lowest common factor of 7 and 9 has, therefore, proven to be a gateway to a rich and fascinating mathematical landscape.
Latest Posts
Latest Posts
-
What Is 1 3 4 In Decimal Form
Mar 31, 2025
-
What Is The Derivative Of X 5
Mar 31, 2025
-
How Many Even Numbers Are On A Dice
Mar 31, 2025
-
What Do Plants Have In Common With Animals
Mar 31, 2025
-
What Is 5 16 In Decimal Form
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Lowest Common Factor Of 7 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
