Log X 4 Solve For X
listenit
May 09, 2025 · 5 min read
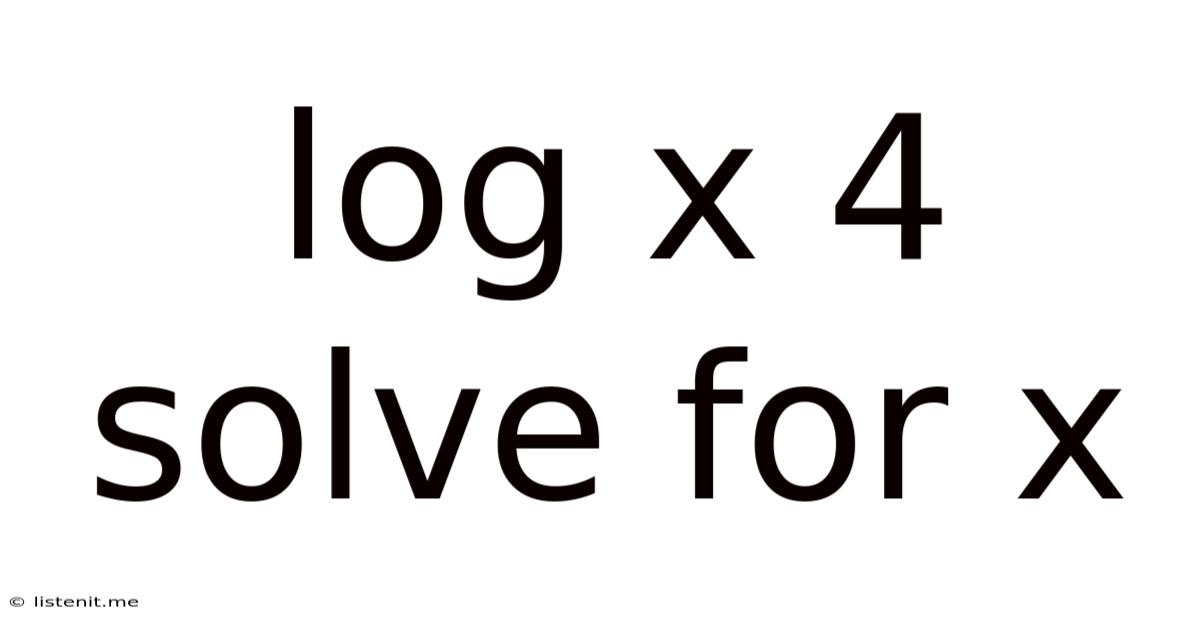
Table of Contents
Solving logₓ4 = 2: A Comprehensive Guide
The equation logₓ4 = 2 might seem simple at first glance, but it opens the door to understanding fundamental concepts in logarithms and exponential functions. This comprehensive guide will not only solve this specific equation but also delve into the underlying principles, providing you with a robust foundation for tackling more complex logarithmic problems. We'll explore different approaches, explain the logic behind each step, and offer practical tips for mastering logarithmic equations.
Understanding the Basics of Logarithms
Before we dive into solving logₓ4 = 2, let's refresh our understanding of logarithms. A logarithm is essentially the inverse operation of exponentiation. The equation logₐb = c is equivalent to the exponential equation aᶜ = b. In this notation:
- a is the base of the logarithm (must be positive and not equal to 1).
- b is the argument (must be positive).
- c is the exponent or logarithm.
In simpler terms, the logarithm answers the question: "To what power must we raise the base (a) to get the argument (b)?"
Solving logₓ4 = 2: Method 1 – Using the Definition of Logarithms
The most straightforward approach to solving logₓ4 = 2 is to directly apply the definition of a logarithm. Recall that logₐb = c is equivalent to aᶜ = b. Therefore, our equation logₓ4 = 2 can be rewritten as:
x² = 4
Now, we need to solve for x. This is a simple quadratic equation. Taking the square root of both sides, we get:
x = ±√4 = ±2
However, the base of a logarithm must always be positive and not equal to 1. Therefore, we must discard the negative solution, x = -2. This leaves us with:
x = 2
Therefore, the solution to the equation logₓ4 = 2 is x = 2.
Solving logₓ4 = 2: Method 2 – Using Change of Base Formula
Another method involves using the change of base formula. This formula allows us to convert a logarithm from one base to another. The change of base formula is:
logₐb = (logₓb) / (logₓa)
where 'x' can be any valid base (commonly 10 or e). Let's apply this to our equation:
logₓ4 = 2
We can rewrite this using a common base, such as base 10:
(log₁₀4) / (log₁₀x) = 2
Now, solve for x:
log₁₀4 = 2 * log₁₀x log₁₀4 = log₁₀(x²) Therefore, 4 = x² x = ±2
Again, since the base of a logarithm must be positive and not equal to 1, we discard the negative solution, resulting in:
x = 2
Verifying the Solution
It's crucial to verify our solution. Substitute x = 2 back into the original equation:
log₂4 = 2
This is equivalent to:
2² = 4
This equation is true, confirming that x = 2 is the correct solution.
Exploring Related Concepts: Properties of Logarithms
Understanding the properties of logarithms is vital for solving more complex logarithmic equations. These properties allow us to manipulate and simplify logarithmic expressions. Here are some key properties:
- Product Rule: logₐ(mn) = logₐm + logₐn
- Quotient Rule: logₐ(m/n) = logₐm - logₐn
- Power Rule: logₐ(mⁿ) = n logₐm
- Change of Base Rule: logₐb = (logₓb) / (logₓa)
- Logarithm of 1: logₐ1 = 0
- Logarithm of the base: logₐa = 1
Solving More Complex Logarithmic Equations
Let's build upon our understanding by tackling a slightly more challenging equation:
log₃(x + 2) + log₃(x - 1) = 2
To solve this, we utilize the product rule:
log₃[(x + 2)(x - 1)] = 2
This simplifies to:
(x + 2)(x - 1) = 3² x² + x - 2 = 9 x² + x - 11 = 0
This is a quadratic equation that can be solved using the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
where a = 1, b = 1, and c = -11. Solving this gives two solutions. However, we must check if both solutions are valid by substituting them back into the original equation. Only solutions that result in positive arguments within the logarithms are valid.
The Importance of Domain Restrictions
When dealing with logarithmic equations, it's critical to remember the domain restrictions. The argument of a logarithm must always be positive. Failing to consider these restrictions can lead to extraneous solutions (solutions that don't satisfy the original equation). Always verify your solutions by substituting them back into the original equation and ensure the arguments of all logarithms are positive.
Practical Applications of Logarithms
Logarithms are not merely abstract mathematical concepts; they have widespread applications across various fields:
- Chemistry: Calculating pH values (a measure of acidity or basicity).
- Physics: Describing radioactive decay and earthquake magnitudes (Richter scale).
- Finance: Modeling compound interest and calculating exponential growth or decay.
- Computer Science: Analyzing algorithms and measuring computational complexity.
- Signal Processing: Working with decibels and analyzing audio signals.
Mastering Logarithmic Equations: Tips and Techniques
- Practice consistently: Solving numerous problems is key to mastering logarithmic equations. Start with simpler problems and gradually increase the complexity.
- Understand the properties of logarithms: A solid grasp of the properties is essential for manipulating and simplifying logarithmic expressions.
- Check your solutions: Always verify your solutions by substituting them back into the original equation and checking for domain restrictions.
- Use multiple methods: Try different approaches to solving the same problem. This reinforces your understanding and helps identify potential errors.
- Utilize online resources: Many online resources offer practice problems and explanations.
Conclusion
Solving logₓ4 = 2 provides a foundational understanding of logarithmic equations. By mastering the concepts discussed in this article, including the definition of logarithms, the change of base formula, and the properties of logarithms, you'll be well-equipped to tackle more complex logarithmic problems. Remember to always verify your solutions and consider the domain restrictions. The widespread application of logarithms across various scientific and technical fields underscores their significance in mathematics and beyond. Consistent practice and a solid understanding of the underlying principles are crucial for success in solving logarithmic equations.
Latest Posts
Latest Posts
-
Graph The Derivative Of The Function Graphed On The Right
May 09, 2025
-
3 To The Power Of 2 As A Fraction
May 09, 2025
-
Graph X 8 On A Number Line
May 09, 2025
-
Is Ethanol Polar Protic Or Aprotic
May 09, 2025
-
Write The Electron Configuration For A Neutral Atom Of Zinc
May 09, 2025
Related Post
Thank you for visiting our website which covers about Log X 4 Solve For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.