Log Ab Log A Log B
listenit
Jun 14, 2025 · 5 min read
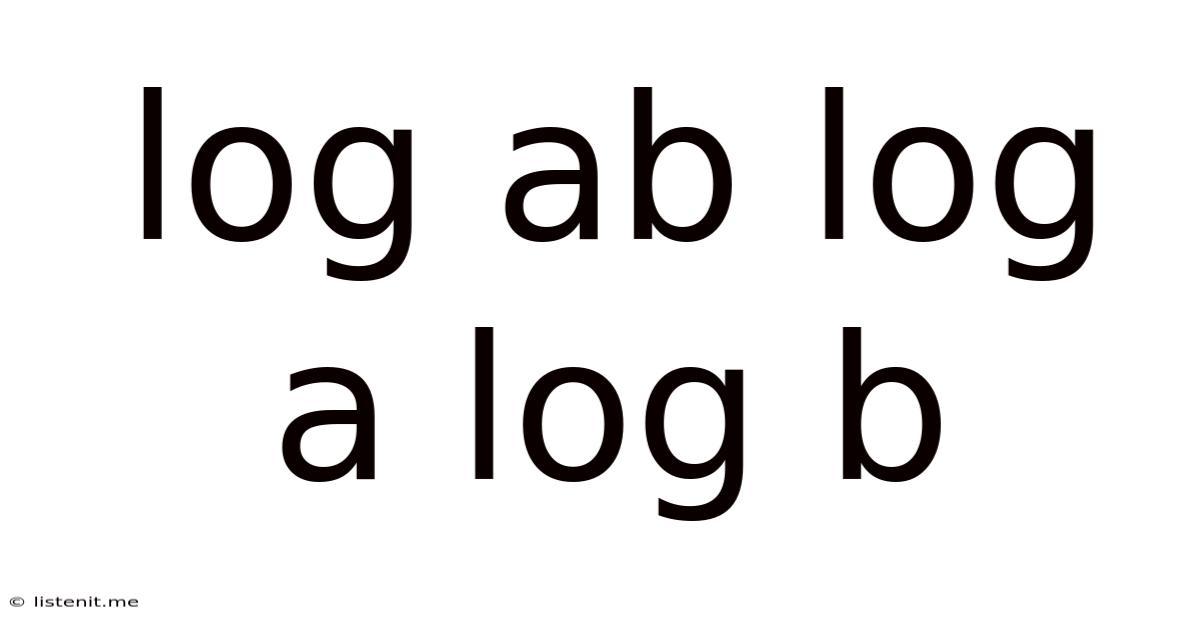
Table of Contents
Decoding the Logarithmic Expression: logₐb logₐlogₐb
The logarithmic expression logₐb logₐlogₐb presents a fascinating challenge in mathematical manipulation and understanding. While seemingly complex, breaking it down into its core components reveals a rich tapestry of logarithmic properties and their applications. This article will delve deep into this expression, exploring its properties, potential simplifications, and practical implications. We will also touch upon related concepts, such as the change of base formula and the importance of understanding logarithmic identities. The goal is to provide a comprehensive guide for anyone seeking to master this specific expression and, more broadly, strengthen their grasp of logarithmic functions.
Understanding the Fundamentals: Logarithms and Their Properties
Before we tackle the complexity of logₐb logₐlogₐb, let's revisit the fundamental concepts of logarithms. A logarithm is essentially the inverse operation of exponentiation. The expression logₐb = x is equivalent to aˣ = b, where:
- a is the base of the logarithm (a > 0, a ≠ 1).
- b is the argument (b > 0).
- x is the exponent or the logarithm itself.
Several key properties govern logarithmic operations, and understanding these is crucial for manipulating and simplifying logarithmic expressions:
1. Product Rule:
logₐ(xy) = logₐx + logₐy
The logarithm of a product is the sum of the logarithms of the individual factors.
2. Quotient Rule:
logₐ(x/y) = logₐx - logₐy
The logarithm of a quotient is the difference between the logarithms of the numerator and the denominator.
3. Power Rule:
logₐ(xⁿ) = n logₐx
The logarithm of a number raised to a power is the product of the power and the logarithm of the number.
4. Change of Base Formula:
logₐb = (logₓb) / (logₓa)
This allows us to change the base of a logarithm from 'a' to any other base 'x', which is particularly useful when working with calculators or software that might only support specific bases (like base 10 or base e).
Analyzing the Expression: logₐb logₐlogₐb
Now, let's dissect the expression logₐb logₐlogₐb. This expression is a composition of logarithmic functions, where the result of the inner logarithm (logₐlogₐb) serves as the argument for the outer logarithm (logₐ). This nested structure introduces an additional layer of complexity.
Important Considerations:
-
Domain Restrictions: Remember that both the base (a) and the arguments (b and logₐb) must be positive, and the base cannot be 1 (a > 0, a ≠ 1, b > 0, logₐb > 0). The condition logₐb > 0 implies that b > 1 if a > 1, and 0 < b < 1 if 0 < a < 1.
-
Numerical Evaluation: The exact numerical value of this expression depends entirely on the values of 'a' and 'b'. There's no general algebraic simplification that eliminates 'a' and 'b' completely. One must substitute specific values for 'a' and 'b' to obtain a numerical result.
-
Approximation Methods: For complex values of 'a' and 'b', numerical methods or computational tools are frequently necessary for evaluation. This often involves utilizing algorithms designed to approximate logarithmic functions efficiently.
Exploring Simplification Strategies
While a complete simplification to a simpler, base-independent form isn't feasible, we can explore potential strategies to manipulate the expression, depending on the context or available information.
Scenario 1: Known Values of 'a' and 'b'
If specific values for 'a' and 'b' are provided, the straightforward approach is direct substitution and calculation. For instance, if a = 10 and b = 100, we can calculate:
log₁₀100 = 2log₁₀(log₁₀100) = log₁₀2≈ 0.301log₁₀(2) * log₁₀(log₁₀100)≈ 0.301 * 0.301 ≈ 0.090601.
Scenario 2: Exploring Relationships Between 'a' and 'b'
If there exists a specific mathematical relationship between 'a' and 'b', it might lead to simplifications. For example, if b = a², then:
logₐb = logₐ(a²) = 2logₐa = 2(because logₐa = 1)logₐ(logₐb) = logₐ2logₐb logₐ(logₐb) = 2 logₐ2
This simplification reveals that the expression can be reduced to a much simpler form under this specific condition. However, such specific relationships are not always present.
Scenario 3: Using Change of Base Formula
The change of base formula could be applied to transform the expression into a different base if it proves computationally advantageous. However, this primarily alters the representation rather than fundamentally simplifying the expression's inherent complexity.
Practical Applications and Real-World Examples
While this specific logarithmic expression might not appear frequently in elementary applications, understanding its components and manipulation techniques is invaluable in several domains:
-
Advanced Calculus: The expression finds use in problems involving integration and differentiation of logarithmic functions and their compositions.
-
Computer Science and Algorithm Analysis: Logarithmic functions often describe the complexity of algorithms, and understanding nested logarithmic expressions can be vital for performance analysis and optimization. For example, algorithms with logarithmic time complexity often involve repeated halving or dividing of the problem size.
-
Signal Processing and Data Analysis: Logarithmic transformations are frequently applied to data to improve its distribution or highlight subtle patterns.
-
Physics and Engineering: Logarithmic scales are used extensively to represent quantities spanning vast ranges (e.g., the Richter scale for earthquakes or the decibel scale for sound intensity).
Conclusion: Mastering the Nuances of Logarithms
The expression logₐb logₐlogₐb serves as a powerful illustration of the complexities and intricacies of logarithmic functions. While a complete universal simplification is unattainable, understanding fundamental logarithmic properties, the conditions for valid operation, and employing strategic manipulation techniques are key to navigating such expressions. The ability to evaluate this expression, given specific values for 'a' and 'b', or to analyze it under specific conditions, showcases a strong grasp of logarithmic principles – a skill applicable across various scientific and computational domains. By mastering the fundamentals and practicing with diverse examples, you can effectively tackle even the most intricate logarithmic expressions. Remember the importance of domain restrictions, and always strive to check your work for accuracy and consistency. The journey into the world of logarithms is rewarding, offering both intellectual stimulation and practical problem-solving skills.
Latest Posts
Latest Posts
-
Nice To Meet You In German
Jun 15, 2025
-
Google Chrome Is Capturing Your Screen
Jun 15, 2025
-
Why Does My Cat Follow Me To The Bathroom
Jun 15, 2025
-
Why Cant You Go Back To Regular Oil After Synthetic
Jun 15, 2025
-
Can You Pray Fajr After Sunrise
Jun 15, 2025
Related Post
Thank you for visiting our website which covers about Log Ab Log A Log B . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.